Графы - одна из базовых структур в теории графов, которая находит свое применение во многих областях, включая математику, физику, компьютерные науки и экономику. Один из основных типов графов - графы Гамильтона. Гамильтоновы графы играют важную роль в различных алгоритмах и задачах, таких как путешествие по городам и поиск оптимальных маршрутов.
Гамильтонов граф - это такой граф, в котором существует гамильтонов цикл, то есть цикл, проходящий по каждой вершине графа ровно один раз. Такой цикл может быть полезен, когда необходимо найти оптимальный маршрут, проходящий через все заданные вершины.
Построение гамильтонова графа - это задача комбинаторной оптимизации, которая часто связана с поиском оптимального маршрута в заданном графе. Существует несколько алгоритмов, позволяющих строить гамильтоновы графы, включая алгоритмы поиска в глубину и алгоритмы на основе динамического программирования.
Знание о гамильтоновых графах и их построении может быть полезно в различных областях, таких как транспортная логистика, маршрутизация сетей и оптимизация планирования задач. Понимание основной концепции гамильтоновых графов и их алгоритмических методов позволяет анализировать и решать сложные задачи в области теории графов и оптимизации маршрутов.
Понятие гамильтонового графа
Для того чтобы построить гамильтонов граф, необходимо выполнить следующие шаги:
- Определить количество вершин в графе и назвать их.
- Составить матрицу смежности, в которой каждому ребру графа будет соответствовать число 1, если вершины соединены, и число 0, если они не соединены.
- Проверить каждую возможную комбинацию пути через вершины, чтобы найти гамильтонов путь или цикл.
- Построить таблицу, в которой приведены вершины и ребра графа. Таблица поможет визуально представить гамильтонов путь или цикл.
- Проанализировать полученные результаты и сделать вывод о наличии или отсутствии гамильтонового пути или цикла в графе.
Гамильтоновы графы широко используются в различных областях, таких как транспортная логистика, коммуникационные сети, планирование маршрутов и других задачах, требующих нахождения оптимального пути через все вершины.
| Вершина | Ребра |
|---|---|
| 1 | 2, 3, 4 |
| 2 | 1, 3, 4 |
| 3 | 1, 2, 4 |
| 4 | 1, 2, 3 |
Значение гамильтонова графа в науке и технике
Гамильтонов граф играет важную роль в различных областях науки и техники, представляя собой удобное математическое средство для моделирования различных систем и задач. Он находит применение в таких областях, как:
1. Транспортная логистика - гамильтонов граф позволяет оптимизировать маршруты и пути перемещения для различных видов транспорта, учитывая ограничения и условия доставки.
2. Сетевое планирование - гамильтонов граф используется для построения оптимальных сетевых структур и планов коммуникации, например, в телекоммуникационных системах и компьютерных сетях.
3. Электроника - гамильтонов граф применяется для проектирования электронных схем, оптимизации расположения элементов и путей прохождения сигналов на микрочипах и других устройствах.
4. Графовые алгоритмы - гамильтонов граф является объектом исследования и разработки различных алгоритмов, таких как поиск и проверка гамильтонова цикла, решение коммивояжерской задачи и других графовых задач.
5. Биоинформатика - гамильтонов граф используется для анализа геномов и протеинов, построения филогенетических деревьев и моделирования биологических процессов.
Таким образом, гамильтонов граф имеет широкое значение в науке и технике как инструмент для решения сложных задач моделирования, оптимизации и анализа различных систем и процессов.
Алгоритмы поиска гамильтоновых циклов
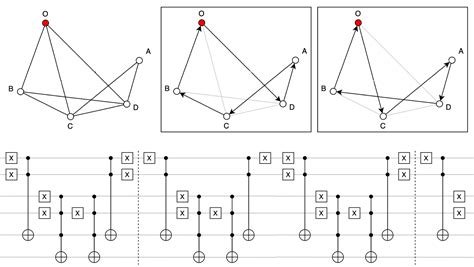
Существует несколько алгоритмов и подходов для поиска гамильтоновых циклов в графе:
- Алгоритм Брон-Кербоша: довольно простой и эффективный алгоритм, основанный на рекурсивном переборе.
- Алгоритмы на основе динамического программирования: эти алгоритмы основаны на разбиении задачи на более маленькие подзадачи и использовании таблиц и матриц для хранения промежуточных результатов.
- Метод ветвей и границ: этот метод основан на итеративном поиске с использованием верхней и нижней границ задачи.
- Методы на основе эвристик: эти методы используют эвристические правила и стратегии для приближенного решения задачи поиска гамильтоновых циклов.
Какой алгоритм использовать для поиска гамильтоновых циклов зависит от многих факторов, таких как размер графа, структура графа и требуемая точность результата. В некоторых случаях, особенно для больших графов, может быть полезно применять комбинацию различных алгоритмов.
Поиск гамильтоновых циклов является важной задачей во многих областях, включая компьютерную науку, физику, биологию и транспортное планирование. Знание различных алгоритмов поиска гамильтоновых циклов позволяет решать сложные задачи и находить оптимальные пути в сетевых структурах.
Построение гамильтоновых графов по заданным условиям
Для построения гамильтоновых графов необходимо определить условия, которым он должен удовлетворять.
- Количество вершин: определите количество вершин, которое должно быть в графе. Все вершины должны быть различными, чтобы в пути не было повторений.
- Соединения между вершинами: определите, какие вершины должны быть соединены ребрами. Для гамильтонового графа каждая вершина должна быть соединена с другой вершиной ребром.
- Направленность ребер: определите, являются ли ребра графа направленными или нет. Это влияет на возможность перемещения по ребрам в обоих направлениях.
Есть несколько алгоритмов, используемых для построения гамильтоновых графов:
- Алгоритм с полным перебором: данный алгоритм исследует все возможные комбинации вершин и ребер до тех пор, пока не будет найден гамильтонов граф. Этот метод гарантирует точное решение, но может потребовать большого количества вычислительных ресурсов.
- Алгоритмы с использованием эвристик: эти алгоритмы используют эвристики и приближенные методы для поиска приемлемых решений в разумное время. Можно использовать алгоритмы на основе генетических алгоритмов или муравьиной оптимизации, чтобы найти гамильтонов граф.
При построении гамильтоновых графов важно учитывать условия и требования конкретной задачи. Некоторые алгоритмы могут быть более эффективными при большом количестве вершин, а другие – при определенных структурах и схемах графа.
В конечном итоге, гамильтонов граф служит важным инструментом для решения различных задач, требующих прохождения пути по всем вершинам графа. Построение гамильтоновых графов по заданным условиям позволяет наглядно представить и анализировать взаимосвязи и зависимости в системе.
Ограничения и сложности задачи поиска гамильтонова цикла

В задаче поиска гамильтонова цикла в графе имеется набор вершин и набор ребер, и требуется найти цикл, проходящий через каждую вершину один раз. На первый взгляд может показаться, что можно просто проверить все возможные циклы, однако количество таких циклов экспоненциально зависит от количества вершин в графе. Это и является основной проблемой в поиске гамильтонова цикла.
Более того, существует несколько известных ограничений и сложностей задачи поиска гамильтонова цикла:
- Сложность алгоритма: Решение задачи поиска гамильтонова цикла в полном графе с n вершинами требует полного перебора (вычислительная сложность O(n!)). Это делает задачу практически неразрешимой при больших значениях n.
- Отсутствие эффективных алгоритмов: На данный момент не существует эффективного алгоритма для решения задачи поиска гамильтонова цикла в произвольном графе.
- Ограничения на графы: Некоторые классы графов могут иметь дополнительные структурные ограничения, что позволяет найти гамильтонов цикл более эффективно. Однако такие классы графов обычно являются специфическими и не охватывают общего случая.
В целом, поиск гамильтонова цикла является одной из самых известных и сложных задач в теории графов. Ее решение имеет важное практическое значение в различных областях, таких как логистика, маршрутизация и планирование. Сложность задачи и отсутствие эффективных алгоритмов требуют поиска альтернативных подходов или применения приближенных методов для решения данной задачи.
Гамильтоновы графы в комбинаторике
В комбинаторике гамильтоновы графы имеют большое значение, так как они позволяют изучать маршруты и циклы в графах с определенными условиями. Решение задач на поиск гамильтоновых путей и циклов в графах может применяться в различных областях, например, в транспортной логистике для оптимизации путей следования или в планировании маршрутов в навигационных системах.
Для построения гамильтонового графа необходимо знать количество вершин, которые он должен содержать, и определить, нужен ли гамильтонов путь или гамильтонов цикл. Затем нужно создать граф с соответствующим количеством вершин и ребер, учитывая условия наличия гамильтонового пути или цикла.
Однако построение гамильтоновых графов является NP-полной задачей и в общем случае не существует эффективного алгоритма для их построения. Поэтому для изучения и решения задач связанных с гамильтоновыми графами часто используются приближенные методы, эвристики и алгоритмы.
Гамильтоновы графы являются важным объектом изучения в комбинаторике и имеют широкий спектр применений. Они позволяют решать задачи связанные с маршрутами и циклами в графах, оптимизировать пути следования и планировать маршруты в различных областях, где важна точность и эффективность передвижения.
Практическое применение гамильтоновых графов в логистике

Гамильтонов граф, который представляет собой граф, в котором можно пройти по всем его вершинам ровно по одному разу, имеет широкое применение в логистике. Это связано с тем, что гамильтонов граф может использоваться для моделирования и оптимизации маршрутов и перевозок.
Одной из ключевых задач логистики является оптимизация процесса доставки товаров от производителя до потребителя. Гамильтонов граф позволяет найти оптимальный маршрут, на котором будут учтены все необходимые точки доставки.
Процесс построения гамильтонова графа в логистике начинается с определения всех точек доставки, которые должны быть учтены в маршруте. Затем строится матрица смежности, которая показывает связи между всеми точками доставки.
С помощью алгоритмов поиска гамильтонова цикла в графе, таких как алгоритмы ближайшего соседа или метод ветвей и границ, можно найти оптимальный маршрут доставки. Это позволяет снизить расходы на топливо, время доставки и повысить эффективность логистической системы.
Кроме того, гамильтоновы графы можно использовать для моделирования и оптимизации комбинаторных задач, связанных с планированием маршрутов доставки, распределением грузов и определением оптимального порядка выполнения задач.
Таким образом, гамильтоновы графы имеют широкое практическое применение в логистике, позволяя оптимизировать процесс доставки, снизить расходы и повысить эффективность логистической системы.
Анализ сложности задачи проверки гамильтоновости
Сложность задачи проверки гамильтоновости зависит от размера графа. Проблема становится NP-полной при росте количества вершин, что означает, что для нахождения оптимального решения требуется экспоненциальное время в худшем случае. Именно поэтому данная задача относится к классу сложных задач.
При анализе сложности задачи проверки гамильтоновости важно учитывать различные методы решения. Существует несколько алгоритмов, которые могут упростить задачу, однако они также требуют высокой вычислительной мощности для работы с большими графами.
Одним из эффективных алгоритмов для проверки гамильтоновости графа является алгоритм Брон-Кербоша. Он базируется на построении всех клик графа и проверке их гамильтоновости. Сложность данного алгоритма также экспоненциальна, однако его применение позволяет найти гамильтонов цикл в некоторых графах за разумное время.
Существует также набор эвристических алгоритмов, которые дают приближенное решение задачи проверки гамильтоновости с более низкой сложностью. Они основаны на эвристических правилах и стратегиях, что позволяет достичь определенного уровня качества решения за меньшее время.
Общая сложность задачи проверки гамильтоновости графа делает ее актуальной для исследования и разработки новых алгоритмов. Такие алгоритмы могут быть полезными в различных областях, включая логистику, транспортную инфраструктуру, сетевой анализ и другие.








