Матрицы – важное понятие в линейной алгебре, которое используется для представления данных и решения различных задач. Одним из важных свойств матриц является их эквивалентность.
Эквивалентными матрицами называются матрицы, которые могут быть получены друг из друга путем элементарных преобразований. Элементарные преобразования включают в себя прибавление к строке (столбцу) другой строки (столбца) с умножением на некоторое число, умножение строки (столбца) на ненулевое число и перестановку строк (столбцов). Главное свойство эквивалентных матриц состоит в том, что они имеют одинаковый ранг - число ненулевых строк (столбцов).
Эквивалентные матрицы позволяют упрощать работу с матрицами и представляют собой мощный инструмент при решении систем линейных уравнений, вычислении определителей и обратных матриц. Благодаря эквивалентности матрицы можно привести к более простому виду и лучше понять структуру и свойства задачи.
Понимание определения и свойств эквивалентных матриц необходимо для работы с линейными преобразованиями, приведения матриц к каноническому (упрощенному) виду и решения различных задач, связанных с линейной алгеброй. Изучение эквивалентных матриц поможет развить навыки логического мышления, абстрактного мышления и аналитического мышления, а также освоить основные методы работы с матрицами.
Что такое эквивалентные матрицы?
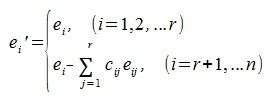
Эквивалентными матрицами называются матрицы, которые могут быть получены друг из друга с помощью элементарных преобразований строк (столбцов) или их комбинаций. Элементарные преобразования строк (столбцов) включают в себя умножение строки (столбца) на ненулевое число, добавление к строке (столбцу) другой строки (столбца), а также перестановку двух строк (столбцов).
Эквивалентные матрицы имеют ряд свойств:
- Они имеют одинаковый ранг.
- Они имеют одинаковые определители.
- Они имеют одинаковые собственные значения.
- Они обладают одинаковыми свойствами относительно операций над матрицами, такими как сложение, умножение, транспонирование и т.д.
Эквивалентные матрицы возникают в различных областях математики и физики, таких как линейная алгебра, теория вероятностей, теория оптимизации и других. Они играют важную роль при решении систем линейных уравнений, нахождении собственных значений и векторов, вычислении определителей и других задачах.
Определение и основные свойства эквивалентных матриц
Основные свойства эквивалентных матриц:
| Свойство | Описание |
|---|---|
| Рефлексивность | Каждая матрица эквивалентна самой себе. |
| Симметричность | Если матрица A эквивалентна матрице B, то матрица B также эквивалентна матрице A. |
| Транзитивность | Если матрица A эквивалентна матрице B и матрица B эквивалентна матрице C, то матрица A также эквивалентна матрице C. |
| Обратимость | Матрицы A и B эквивалентны, если A может быть получена из B и B может быть получена из A путем выполнения одних и тех же элементарных преобразований строк и столбцов. |
| Совместимость с операциями | Сложение эквивалентных матриц даёт эквивалентную матрицу, а умножение эквивалентной матрицы на произвольную матрицу также даёт эквивалентную матрицу. |
Знание определения и свойств эквивалентных матриц позволяет упростить операции над матрицами и обнаруживать их особенности и зависимости.
Условия эквивалентности матриц

Матрицы A и B называются эквивалентными, если они могут быть получены друг из друга путем конечного числа элементарных преобразований.
Элементарные преобразования над матрицей включают:
- Умножение строки на ненулевое число.
- Прибавление к одной строке другой строки, умноженной на число.
- Перестановку двух строк местами.
Для того чтобы две матрицы A и B были эквивалентными, необходимо и достаточно, чтобы они имели одно и то же число строк и столбцов, и было возможно с помощью элементарных преобразований привести одну матрицу к другой.
Примеры эквивалентных матриц
Вот несколько примеров эквивалентных матриц:
Пример 1:
Матрица A:
1 2 3 4 5 6 7 8 9
Матрица B:
1 0 0 0 1 0 0 0 1
Для получения матрицы B из матрицы A были выполнены следующие преобразования:
1. Строка 2 была заменена на сумму строки 2 и строки 1, умноженную на -4.
2. Строка 3 была заменена на сумму строки 3 и строки 1, умноженную на -7.
Пример 2:
Матрица C:
1 2 3 4 5 6 7 8 9
Матрица D:
1 2 3 0 -3 -6 0 0 0
Матрица E:
1 2 3 0 1 2 0 0 0
Матрица F:
1 0 -1 0 1 2 0 0 0
Матрицы D, E и F являются эквивалентными матрицами матрицы C. Для получения каждой из них были выполнены элементарные преобразования строк.
Эти примеры иллюстрируют основное свойство эквивалентных матриц: они представляют одну и ту же линейную систему уравнений. Понимание эквивалентных матриц позволяет нам легче решать системы линейных уравнений и использовать их в контексте линейных преобразований.








