Эквивалентное множество - это особое понятие в математике, которое означает, что два или более множества имеют одинаковую мощность, то есть содержат одинаковое количество элементов. Это означает, что существует взаимно однозначное соответствие между элементами этих множеств, и каждому элементу одного множества соответствует единственный элемент другого множества.
Определить, являются ли два множества эквивалентными, можно с помощью функции-сопоставления, которая устанавливает соответствие между элементами множеств. Если такая функция существует, то множества считаются эквивалентными. Эту функцию называют биекцией.
Например, рассмотрим множество натуральных чисел {1, 2, 3, 4, ...} и множество четных натуральных чисел {2, 4, 6, 8, ...}. Множества могут быть представлены функцией f(n) = 2n, где n - элемент из первого множества, а 2n - элемент из второго множества. Эта функция устанавливает взаимно однозначное соответствие между элементами двух множеств и является биекцией.
Определение эквивалентности множеств имеет важное значение в различных областях математики, например, в теории множеств, алгебре, топологии и других. Эта концепция помогает установить равномощность множеств и решать различные задачи, связанные с их свойствами и взаимодействиями.
Эквивалентное множество - определение и понятие

Определение эквивалентного множества возможно на основе различных критериев или условий, которые соответствуют задаче или контексту. Например, в математике два множества считаются эквивалентными, если между их элементами можно установить взаимно-однозначное соответствие. В лингвистике эквивалентные множества могут состоять из схожих языковых выражений или семантических единиц.
Определение эквивалентного множества играет важную роль в различных областях знания. Оно позволяет устанавливать сходство или сопоставлять различные объекты, явления или процессы. Эквивалентные множества могут использоваться для упрощения задач, классификации или поиска аналогий. Также наличие эквивалентных множеств может быть полезно при изучении новых языков, культур и традиций.
В заключение, эквивалентное множество представляет собой совокупность элементов, которые обладают общими свойствами или сопоставимыми характеристиками. Выявление и определение таких множеств позволяет установить сходство и создать основу для сравнительного анализа. Это важная концепция, которая находит применение в различных областях знания и исследований.
Что такое эквивалентное множество?
Например, рассмотрим множество студентов, где каждый студент представлен своим именем и оценкой по некоторому предмету. Если мы хотим найти эквивалентные множества студентов с одинаковыми оценками, мы должны определить отношение эквивалентности между студентами: два студента эквивалентны, если у них одинаковая оценка. Таким образом, каждое эквивалентное множество будет состоять из студентов с одинаковым результатом по предмету.
Для определения эквивалентных множеств необходимо:
- Определить критерий или отношение, на основе которого будет проверяться эквивалентность элементов.
- Применить этот критерий к элементам множества и сгруппировать эквивалентные элементы в отдельные подмножества.
Такое группирование элементов множества в эквивалентные множества позволяет производить операции над ними относительно этих групп вместо индивидуальных элементов, что может быть полезно при решении определенных задач или анализе данных.
Основные свойства эквивалентного множества
Эквивалентное множество обладает рядом важных свойств, которые позволяют определить его и использовать в различных областях:
1. Рефлексивность: каждый элемент эквивалентного множества связан с самим собой. Это означает, что для любого элемента x из множества, x будет эквивалентен x (x ~ x).
2. Симметричность: если два элемента связаны отношением эквивалентности, то они можно менять местами без изменения смысла. То есть, если x ~ y, то и y ~ x.
3. Транзитивность: если первый элемент связан с вторым, а второй элемент связан с третьим, то первый элемент также связан с третьим. Формально, если x ~ y и y ~ z, то и x ~ z.
4. Каждый элемент множества принадлежит ровно одному классу эквивалентности. Класс эквивалентности - это множество всех элементов, которые связаны друг с другом отношением эквивалентности.
Эти свойства эквивалентного множества позволяют определить его уникальность и использовать его для классификации объектов или установления отношений между ними.
Как определить эквивалентное множество?
Для определения эквивалентного множества необходимо выполнить следующие шаги:
- Выбрать два множества для сравнения.
- Проверить, что каждый элемент из одного множества принадлежит другому множеству, и наоборот. Это значит, что каждый элемент из первого множества должен содержаться во втором множестве, и каждый элемент из второго множества должен содержаться в первом множестве.
- Если каждый элемент из одного множества принадлежит другому, то множества считаются эквивалентными. Если хотя бы один элемент не содержится в другом множестве, то множества считаются неэквивалентными.
Например, рассмотрим два множества: A = {1, 2, 3} и B = {2, 3, 4}. Для определения эквивалентности этих множеств, нужно проверить, что каждый элемент из множества A содержится в множестве B, и каждый элемент из множества B содержится в множестве A. В данном случае, элементы 2 и 3 содержатся и в множестве A, и в множестве B. Однако, элементы 1 и 4 не содержатся в обоих множествах. Поэтому множества A и B не являются эквивалентными.
Равномощные множества и их связь с эквивалентным множеством
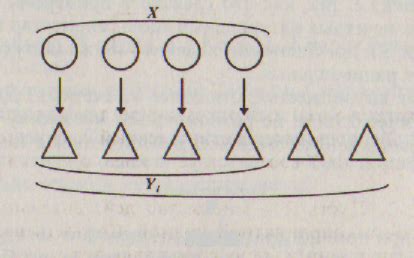
Для определения равномощности множеств, необходимо установить биекцию между ними. Биекция – это отображение, которое является одновременно инъекцией и сюръекцией. Инъекция означает, что каждому элементу множества отображения соответствует ровно один элемент в множестве приемника. Сюръекция означает, что каждый элемент множества приемника имеет хотя бы одно соответствующее значение в множестве отображения. Если между двумя множествами существует биекция, то они считаются равномощными.
Связь равномощных множеств с эквивалентным множеством состоит в том, что эквивалентное множество является подмножеством равномощного множества, но не обязательно содержит все его элементы. Эквивалентное множество – это такое подмножество равномощного множества, которое содержит только некоторые его элементы. То есть они имеют одинаковый объем, но не обязательно полностью совпадают.
| Равномощные множества | Эквивалентное множество |
|---|---|
| Множество натуральных чисел | Множество четных натуральных чисел |
| Множество действительных чисел | Множество рациональных чисел |
| Множество простых чисел | Множество квадратных чисел |
Таким образом, равномощные множества имеют соответствие между всеми элементами, в то время как эквивалентное множество содержит только часть элементов равномощного множества.
Примеры эквивалентных множеств
Эквивалентные множества представляют собой два или более разных множества, состоящих из элементов, которые имеют одинаковые характеристики или свойства. Эти множества могут быть разных размеров и иметь различные элементы, но все равно считаются эквивалентными в контексте определенного критерия.
Вот несколько примеров эквивалентных множеств:
| Множество A | Множество B | Эквивалентность |
|---|---|---|
| {1, 2, 3} | {4, 5, 6} | Не эквивалентны |
| {1, 2, 3} | {3, 2, 1} | Эквивалентны |
| {apple, banana, orange} | {banana, orange, apple} | Эквивалентны |
| {a, b, c} | {d, e, f} | Не эквивалентны |
Как видно из примеров, порядок элементов в множествах не имеет значения для определения их эквивалентности. Кроме того, элементы могут повторяться в этих множествах, но это не влияет на их эквивалентность.
Определение эквивалентности множеств основывается на сравнении элементов и их характеристик. Если все элементы одного множества имеют эквивалентные элементы в другом, то эти множества считаются эквивалентными.
Практическое применение эквивалентных множеств

Эквивалентные множества находят свое практическое применение в различных областях, включая математику, логику, информатику и другие науки.
Одно из практических применений эквивалентных множеств в математике заключается в обобщении и облегчении работы с различными структурами данных. Например, при работе с графами, можно использовать эквивалентные множества для эффективного поиска связей между вершинами. Это позволяет ускорить алгоритмы, работающие с графами, и упростить анализ их свойств.
В логике эквивалентные множества используются для определения и анализа эквивалентных утверждений. Если два утверждения эквивалентны, то они имеют одинаковые логические значения во всех ситуациях. Это позволяет сократить сложность рассуждений и упростить логические доказательства и выводы.
В информатике эквивалентные множества находят применение в алгоритмах объединения и поиска. Например, алгоритм "Quick Find" использует эквивалентные множества для быстрого определения связей между элементами массива.
Также эквивалентные множества могут использоваться для классификации и группировки данных. Например, при анализе социальных сетей можно применить эквивалентные множества для определения групп пользователей, имеющих общие интересы или связи. Это помогает в анализе и предсказании поведения в сети и оптимизации работы веб-сервисов.
Таким образом, практическое применение эквивалентных множеств не ограничивается только математикой, оно расширяется на различные области, где требуется классификация, поиск связей или оптимизация алгоритмов.
Сложность определения эквивалентного множества
Определение эквивалентного множества может быть сложной задачей, особенно в случае больших и сложных наборов данных. Возникают несколько основных проблем, которые могут усложнить этот процесс:
- Большое количество элементов: Если множество содержит много элементов, то каждому элементу в множестве потребуется проверка на эквивалентность с другими элементами. Это может быть вычислительно затратной задачей, особенно при наличии большого количества данных.
- Сложность элементов: Если элементы в множестве имеют сложную структуру или представляют собой объекты с большим количеством свойств или атрибутов, то определение их эквивалентности может потребовать дополнительных шагов и вычислений.
- Определение условий эквивалентности: Критерии, по которым определяется эквивалентность элементов, могут различаться в зависимости от контекста. Не всегда существует четкое определение того, что делает два элемента эквивалентными, и это требует проведения дополнительных анализов и определения правил для проверки эквивалентности.
- Чувствительность к порядку: Некоторые множества могут быть чувствительны к порядку элементов. Это может усложнить определение эквивалентного множества, поскольку изменение порядка элементов может привести к изменению эквивалентности.
Учитывая все эти факторы, определение эквивалентного множества может быть нетривиальной задачей, которая требует аккуратного анализа данных и выбора подходящего алгоритма для определения эквивалентности элементов.
Теорема о классах эквивалентности
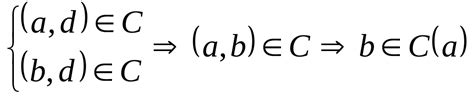
Более формально, пусть дано множество X и отношение эквивалентности R на нем. Тогда класс эквивалентности элемента x обозначается как [x] и определяется как множество всех элементов, эквивалентных x. Множество классов эквивалентности обозначается как X/R.
Теорема о классах эквивалентности утверждает, что множество X/R образует разбиение множества X, то есть:
| Свойство | Определение |
|---|---|
| Непустота | Множество X/R не пусто, то есть содержит хотя бы один класс эквивалентности. |
| Изолированность | Различные классы эквивалентности не пересекаются, то есть для любых двух различных классов [x] и [y] выполняется [x] ∩ [y] = ∅, где ∅ обозначает пустое множество. |
| Индуктивное свойство | Объединение всех классов эквивалентности составляет множество X, то есть X = ∪[x], где символ ∪ обозначает объединение множеств. |
Таким образом, теорема о классах эквивалентности позволяет разбить множество на непересекающиеся классы, в каждом из которых элементы равны друг другу согласно заданному отношению эквивалентности. Это понятие является одним из основных в теории множеств и широко применяется в различных областях математики и информатики.








