Что значит эйлеров граф

Эйлеров граф – это то, что мы получаем, если соединим все вершины графа таким образом, что каждое ребро будет пройдено ровно один раз. Такой граф назван в честь выдающегося швейцарского математика Леонарда Эйлера, который первым дал определение и изучал свойства таких графов в конце XVIII века.

Эйлеров граф обладает некоторыми интересными свойствами. Во-первых, в нем количество вершин нечётной степени (количество рёбер, выходящих из вершины) может быть равным лишь нулю или двум. Во-вторых, граф является связным, то есть существует путь между любой парой его вершин.

Самой известной задачей, связанной с Эйлеровым графом, является задача о

семи кёнигсбергских мостах

. В Кёнигсберге (ныне это Калининград) находился остров с рекой Прегель, на котором было четыре части семейственных участков и семь мостов, соединяющих их. Вопрос был в следующем: можно ли пройти по каждому мосту так, чтобы пройти по нему ровно один раз и вернуться в исходную точку? Доказательство невозможности этой задачи было одним из самых первых приложений Эйлеровой теории к реальной жизни.

Определение графа Эйлера

Графом Эйлера называется граф, который содержит цикл, проходящий по каждому ребру ровно один раз. Такой цикл называется эйлеровым циклом. Эйлеров граф может быть как ориентированным, так и неориентированным.

Основная особенность графа Эйлера состоит в том, что он содержит ребра, которые можно пройти только один раз и вернуться в исходную вершину. Другими словами, в эйлеровом графе существует путь, который проходит по каждому ребру ровно один раз и заканчивается в исходной вершине.

Определение графа Эйлера было предложено известным швейцарским математиком Леонардом Эйлером в XVIII веке. С тех пор эйлеровы графы нашли широкое применение в различных областях науки и инженерии, включая транспортное планирование, сетевой анализ, компьютерные алгоритмы и многое другое.

Важно отметить, что не все графы являются эйлеровыми. Существуют определенные условия и ограничения, при которых граф может быть классифицирован как эйлеров.

Основные свойства Эйлеровых графов

Основные свойства Эйлеровых графов:

1. Эйлеров граф содержит все вершины степени четное число, за исключением, возможно, двух вершин степени нечетное число (начальной и конечной вершины, если граф является эйлеровым путем).
2. Если граф связный и все его вершины имеют степень четное число, то он является эйлеровым циклом.
3. Если граф связный, все вершины кроме двух имеют степень четное число, а две вершины имеют степень нечетное число, то он является эйлеровым путем, началом и концом которого являются вершины с нечетными степенями.
4. Эйлеровы графы также могут быть взвешенными, когда каждое ребро имеет вес или стоимость, и задача заключается в нахождении Эйлерова пути или цикла минимального веса.

Примерами Эйлеровых графов могут служить сети электропередачи, где граф представляет собой систему линий передачи, а ребра - линии электропередачи. Также Эйлеровы графы находят применение в транспортных сетях, логистике и других областях, связанных с оптимизацией маршрутов.

Как определить, является ли граф Эйлеровым

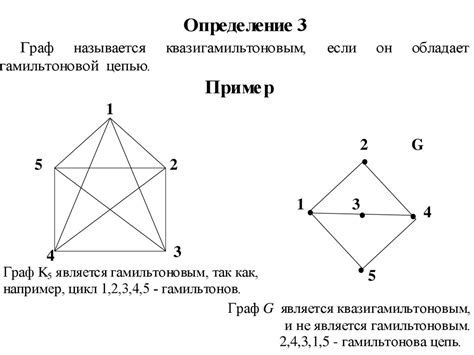
Граф Эйлеровым называется граф, который содержит эйлеров цикл, то есть путь, проходящий по каждому ребру графа ровно один раз и возвращающийся в исходную вершину.

Существует несколько критериев, позволяющих определить, является ли граф Эйлеровым:

• Граф связный и все его вершины имеют четную степень.
• Граф связный и имеет ровно две вершины нечетной степени.
• Граф связный и все его вершины имеют четную степень, за исключением двух, которые имеют нечетную степень.

Если заданный граф удовлетворяет одному из этих критериев, то он является Эйлеровым. В противном случае граф не является Эйлеровым.

Например, рассмотрим граф, изображенный на рисунке:

Вставить изображение графа

В данном случае, все вершины графа имеют степень 2, поэтому он является Эйлеровым.

Количество рёбер и вершин в Эйлеровом графе

В Эйлеровом графе количество рёбер и вершин может быть различным. Общее количество вершин и рёбер в графе зависит от его конкретной структуры и свойств. Однако, есть некоторые общие правила, которые можно применять для определения количества вершин и рёбер в Эйлеровом графе.

Если в Эйлеровом графе имеется эйлеров цикл (такой путь, который проходит по каждому ребру графа ровно один раз), то количество вершин и рёбер в графе будет равно. Это следует из того, что каждая вершина будет являться началом и концом ребра, и поэтому каждая вершина будет иметь одинаковую степень (количество рёбер, связанных с данной вершиной). Общее количество вершин и рёбер в таком графе можно найти по формуле: V = E + 1, где V - количество вершин, а E - количество рёбер.

Если же в Эйлеровом графе отсутствует эйлеров цикл, то количество вершин и рёбер в графе будет различным. В этом случае количество рёбер обычно оказывается больше количества вершин. Например, в Эйлеровом графе с двумя вершинами и тремя рёбрами количество рёбер больше на 1, чем количество вершин. Однако, такие случаи редки и в основном в Эйлеровых графах количество вершин и рёбер близко друг к другу.

Таким образом, количество рёбер и вершин в Эйлеровом графе зависит от наличия эйлерова цикла. Если цикл присутствует, то количество вершин и рёбер будет равно, иначе количество рёбер будет превышать количество вершин.

Существование эйлерова цикла и эйлерова пути

Для существования эйлерова цикла в графе необходимо и достаточно выполнение следующих условий:

1. Граф должен быть связным, то есть из любой вершины можно попасть в любую другую вершину по ребру.

2. У всех вершин графа должны быть четные степени. Степень вершины - количество ребер, смежных с данной вершиной. Таким образом, все вершины графа должны иметь четное количество ребер, иначе граф не будет иметь эйлерова цикла.

Если в графе не выполняется условие четной степени для всех вершин, но условие связности выполняется, то возможно существование эйлерова пути. Эйлеров путь - это путь, который проходит через все ребра графа ровно один раз, но не обязательно возвращается в исходную вершину.

Существование эйлерова пути в графе обусловлено следующими условиями:

1. Граф должен быть связным.

2. У только двух вершин графа должны быть нечетные степени, все остальные вершины должны иметь четные степени. Таким образом, эйлеров путь начинается в одной вершине, проходит через все ребра графа, и заканчивается в другой вершине.

Случаи, когда граф не является Эйлеровым

В некоторых случаях граф может не быть Эйлеровым, то есть в нем может не существовать эйлерова цикла или эйлерова пути.

Одним из таких случаев является наличие вершин степени нечетного числа. В эйлеровом графе степень каждой вершины должна быть четной, поскольку при прохождении по ребрам графа каждый раз "вход" и "выход" из вершины учитываются, и если степень вершины нечетная, то она не сможет быть включена в эйлеров путь или цикл.

Другой случай, когда граф не является Эйлеровым, - это разделение графа на несколько крупных компонент связности. Если граф имеет несколько отдельных компонент, то для того чтобы существовал эйлеров путь или цикл, каждая компонента должна содержать нечетное количество вершин, поскольку каждый раз, когда мы переходим из одной компоненты в другую, учитывается "вход" и "выход" из вершины. Если количество вершин в каждой компоненте связности четное, то невозможно построить эйлеров путь или цикл.

Также, если граф является ориентированным, то он может не быть Эйлеровым в случае, если степень "входа" в каждую вершину не равна степени "выхода" из нее. В эйлеровом графе степень каждой вершины должна быть равна, поскольку при прохождении по ребрам графа каждый раз "вход" и "выход" из вершины учитываются.

Если граф не удовлетворяет хотя бы одному из этих условий, то он не является Эйлеровым.

Пример Эйлерового графа: циклу Эйлера

Рассмотрим пример графа и его цикла Эйлера:

Граф:

A------B
/|     /|
/ |    / |
/  |   /  |
D---+--C   |
|   |  |   |
|   H--|---G
|  /   |  /
| /    | /
|/     |/
E------F

В данном примере, граф содержит 8 вершин (A-H) и 12 ребер. Чтобы найти цикл Эйлера в этом графе, необходимо пройти по всем его ребрам, используя каждое ребро только один раз и вернуться в исходную вершину. В нашем случае, возможный цикл Эйлера будет следующим: A-B-C-G-H-F-E-D-A.

Цикл Эйлера является важным понятием в теории графов и находит применение в различных задачах, таких как задачи о коммивояжере, планирование маршрутов и других.

Пример Эйлерового графа: пути и циклы

Рассмотрим следующий пример графа:

• Вершины: A, B, C
• Ребра: AB, AC, BC, BA, CA, CB

В данном примере, каждая вершина связана со всеми другими вершинами ребром. Таким образом, в этом графе существует путь, проходящий по всем ребрам графа ровно один раз, такой путь называется Эйлеровым путем. В данном случае, возможны следующие Эйлеровы пути:

1. AB-BC-CA-AC-CB-BA
2. BA-AC-CB-BC-CA-AB
3. AC-CA-AB-BC-CB-BA

Также в этом графе существует цикл, проходящий по всем ребрам графа ровно один раз, такой цикл называется Эйлеровым циклом. В данном случае, возможен следующий Эйлеров цикл:

AB-BC-CA-AC-CB-BA-AB

Таким образом, данный граф является Эйлеровым графом, так как в нем существует Эйлеров цикл.

Пример Эйлерового графа: графы с несколькими компонентами связности

Графы с несколькими компонентами связности имеют несколько изолированных групп вершин, между которыми нет ребер. Все компоненты связности можно рассматривать независимо друг от друга. Чтобы граф являлся Эйлеровым, каждая компонента связности должна быть Эйлеровым графом.

Рассмотрим пример графа с двумя компонентами связности:

Компонента 1 Вершины: A, B, C Ребра: AB, BC

Компонента 2 Вершины: D, E Ребра: DE

Для того чтобы этот граф был Эйлеровым, каждая компонента связности должна быть Эйлеровым графом. Рассмотрим компоненту 1. В этой компоненте все вершины имеют нечетную степень, поэтому в ней нет Эйлерова цикла. Таким образом, компонента 1 не является Эйлеровым графом.

Теперь рассмотрим компоненту 2. У вершин D и E степень равна 1, поэтому в ней есть Эйлеров цикл: DE. Значит, компонента 2 является Эйлеровым графом.

Таким образом, граф с двумя компонентами связности не является Эйлеровым графом, так как одна из компонент не является Эйлеровым графом.

Алгоритм построения Эйлерова пути в графе

1. Выбирается вершина графа, из которой выходят нечетное количество ребер.
2. Строится произвольный путь из этой вершины по ребрам графа до следующей вершины с нечетным количеством ребер.
3. По очереди добавляются все пройденные ребра в Эйлеров путь.
4. Из участка пути, который был добавлен в пункте 3, удаляются все использованные ребра, а вершина, из которой они выходили, добавляется в стек.
5. Шаг 2-4 повторяется, пока не будут добавлены все ребра графа.
6. Когда все ребра будут добавлены в путь, в стеке окажутся вершины, не посещенные полностью. Из этих вершин происходит переход к следующей вершине с нечетным количеством ребер, и процесс повторяется снова.

Использование этого алгоритма позволяет найти Эйлеров путь в любом связном графе с не более чем двумя вершинами нечетной степени. Если в графе есть вершины с нечетной степенью больше двух, Эйлеров путь не существует.

Алгоритм построения Эйлерова пути в графе имеет множество модификаций и вариаций, в зависимости от конкретной задачи и структуры графа. Его применение позволяет эффективно решать различные задачи, связанные с обходом графов и поиску оптимальных путей.