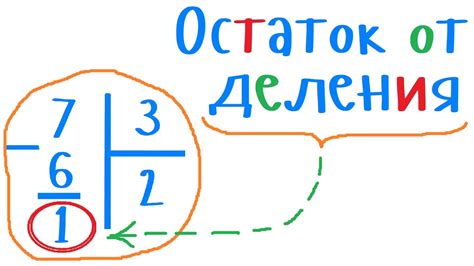
Деление по модулю – это операция в математике, которая позволяет определить остаток от деления одного числа на другое. Остаток от деления может быть положительным или отрицательным числом и всегда меньше делителя. Операция деления по модулю обозначается знаком %.
Остаток от деления по модулю широко используется в различных сферах, включая программирование. Например, остаток от деления по модулю может быть использован для определения четности или нечетности числа. Если остаток от деления числа на 2 равен 0, то число является четным, в противном случае – нечетным.
Деление по модулю также полезно для решения задач, связанных с периодичностью. Например, задача о круговой очередности – когда нужно определить следующий элемент в последовательности, перейдя от последнего к первому и так далее. Деление по модулю помогает определить порядок элементов в таких последовательностях.
Определение и понятие

Для обозначения операции деления по модулю используется символ % или mod. Например, выражение a % b или a mod b, где a и b - целые числа, обозначает деление числа a на число b и возвращает остаток от этого деления.
Операция деления по модулю широко применяется в программировании. Например, она может использоваться для определения четности или нечетности числа, проверки на кратность, циклического обхода элементов массива и других задач.
Простые числа и деление по модулю
Простым числом называется число, которое делится только на 1 и на само себя без остатка. Например, числа 2, 3, 5, 7 являются простыми, так как они не делятся ни на какие другие числа кроме 1 и самих себя.
Чтобы определить, является ли число простым или составным, можно использовать деление по модулю. Деление по модулю представляет собой операцию, при которой получаем остаток от деления одного числа на другое. Если при делении числа на все числа от 2 до корня из этого числа остаток равен нулю, то число является составным, в противном случае - простым.
Пример: Пусть нам нужно проверить, является ли число 17 простым. Делим 17 по модулю на все числа от 2 до корня из 17 (4), т.е. на 2 и 3. Получаем следующие остатки: 17%2=1, 17%3=2. Ни один из остатков не равен нулю, поэтому число 17 является простым.
Простые числа играют важную роль в криптографии и алгоритмах шифрования. Например, RSA-шифрование использует простые числа для генерации публичных и приватных ключей. Деление по модулю помогает проверить, что числа, используемые в шифровании, являются простыми и обеспечивает безопасность системы.
| Примеры простых чисел | Примеры составных чисел |
|---|---|
| 2 | 4 |
| 3 | 6 |
| 5 | 8 |
| 7 | 9 |
Когда применяется деление по модулю в математике
Одной из основных областей, где используется деление по модулю, является теория чисел. Эта область исследует свойства чисел и арифметические операции над ними. В теории чисел деление по модулю используется, например, для проверки делимости чисел или для определения периодичности некоторых десятичных дробей.
В алгебре деление по модулю также может применяться для решения различных задач. Например, в криптографии это используется для создания криптографических хеш-функций, которые обеспечивают защиту информации.
Деление по модулю может применяться и в программировании. В языках программирования такие операторы, как % (процент), позволяют выполнять операцию деления по модулю. Это может быть полезно, например, для проверки, является ли число четным или нечетным, или для перевода некоторых величин в другие системы счисления.
Таким образом, деление по модулю является важной и полезной математической операцией, которая находит применение в различных областях математики, алгебры и программирования.
Применение деления по модулю в программировании
Деление по модулю имеет широкое применение в программировании и играет важную роль в различных алгоритмах и задачах. Ниже приведены некоторые области, где применяется деление по модулю:
- Проверка на четность и нечетность числа: Деление числа на 2 с помощью операции модуля позволяет определить, является ли число четным или нечетным. Если результат деления равен 0, число является четным, иначе - нечетным.
- Хэширование и циклические структуры данных: Деление по модулю используется в хэш-функциях для равномерного распределения значений по массиву (хэш-таблице). Также оно позволяет обрабатывать циклические структуры данных, такие как кольцевые буферы или кольцевые списки.
- Определение периодичности последовательностей: Деление по модулю позволяет определить периодичность последовательности чисел. Например, если мы делим каждый элемент последовательности на некоторое число и получаем одинаковые остатки, то последовательность является периодичной.
- Работа с календарями: Деление по модулю используется для определения дня недели или других циклических периодов в календарях. Например, можно определить день недели для заданной даты, разделив порядковый номер дня на количество дней в неделе и взяв остаток от деления.
- Генерация случайных чисел: Деление по модулю может быть использовано для генерации случайных чисел в некотором заданном диапазоне. Например, если у нас есть случайное число rand, мы можем получить случайное число от 0 до N, взяв остаток от деления rand на N+1.
Это лишь некоторые примеры применения деления по модулю в программировании. Этот математический оператор широко используется в различных областях и является важным инструментом для манипуляции с числами и структурами данных.
Проверка чисел на четность и нечетность

При обозначении деления по модулю используется знак процента (%). Операция деления по модулю возвращает остаток от деления одного числа на другое. Например, если число 7 делится на 2, то остаток от деления будет равен 1, что означает, что число 7 является нечетным.
Проверка чисел на четность и нечетность является очень полезной при программировании. Например, чтобы проверить, является ли число, введенное пользователем, четным или нечетным, можно использовать операцию деления по модулю и условные операторы.
Шифрование данных с использованием деления по модулю
Процесс шифрования с использованием деления по модулю может быть представлен следующим образом: выбирается открытый ключ, состоящий из двух чисел - простого числа p и положительного целого числа g, которое является примитивным корнем по модулю операции. Затем, каждому буквенному символу сообщения присваивается числовое значение, а затем применяется операция деления по модулю p. Таким образом, каждому символу сообщения соответствует шифрованное число.
Шифрование данных с использованием деления по модулю обладает свойством односторонней функции, что означает, что сложно восстановить исходные данные из зашифрованного значения без знания открытого ключа. Это делает этот метод шифрования надежным и устойчивым к взлому.
Шифрование данных является важным средством защиты информации при передаче по сети или при хранении на устройствах. Использование деления по модулю для шифрования данных позволяет обеспечить конфиденциальность и безопасность передаваемых или хранимых данных.
Генерация псевдослучайных чисел с помощью деления по модулю

Деление по модулю представляет собой операцию нахождения остатка от деления одного числа на другое. В контексте генерации псевдослучайных чисел, деление по модулю может быть использовано для получения целочисленных значений в заданном диапазоне.
Для генерации чисел с помощью деления по модулю, необходимо выбрать два числа: начальное значение (сид) и модуль. Сид является исходной точкой для генерации последовательности чисел, а модуль определяет диапазон возможных значений.
Алгоритм генерации псевдослучайных чисел с помощью деления по модулю следующий:
| Шаг | Описание |
|---|---|
| 1 | Выбрать начальное значение (сид) |
| 2 | Выбрать модуль |
| 3 | Выполнить операцию деления по модулю числа сида на модуль |
| 4 | Получить остаток от деления |
| 5 | Использовать полученный остаток как новое значение сида и повторить шаги 3-5, чтобы сгенерировать последующие числа |
Таким образом, при каждой итерации алгоритма получается новое псевдослучайное число в заданном диапазоне, исходя из текущего значения сида и модуля.
Однако стоит отметить, что генерация псевдослучайных чисел с помощью деления по модулю не является криптографически стойким методом. Некорректное выбор сида и модуля может привести к плохой случайности и предсказуемости последовательности чисел.
Вывод: генерация псевдослучайных чисел с помощью деления по модулю является простым и эффективным методом, который может быть использован в различных приложениях. Однако для обеспечения высокой случайности и стойкости к взлому необходимо выбирать с учетом особых требований и рекомендаций.
Работа с циклическими структурами данных при делении по модулю
При делении по модулю обычно используется оператор % (процент), который возвращает остаток от деления одного числа на другое. Однако при работе с циклическими структурами данных такие операции могут иметь особенности и требовать специального подхода.
Рассмотрим пример использования деления по модулю для работы с числами в круговом порядке. Например, у нас есть круг из 12 чисел (1, 2, 3, ..., 12), и мы хотим определить, следующее число в этой последовательности после заданного числа.
Для этого мы можем воспользоваться операцией деления по модулю. Например, если нам известно, что текущее число равно 9, мы можем вычислить следующее число следующим образом:
int currentNumber = 9; // текущее число int nextNumber = (currentNumber + 1) % 12; // следующее число
В этом примере мы добавляем единицу к текущему числу и применяем операцию деления по модулю на 12. Остаток от деления будет равен следующему числу в круговой последовательности. В данном случае, следующее число будет равно 10.
Таким образом, деление по модулю позволяет нам эффективно работать с циклическими структурами данных, такими как круговые последовательности, циклические массивы, циклические списки и т.д. Это может быть полезно, например, при реализации алгоритмов обхода графов, перебора элементов в круговом порядке и других задачах, где необходимо учитывать цикличность данных.
Использование деления по модулю в криптографии
Деление по модулю, также известное как операция нахождения остатка от деления, имеет широкое применение в криптографии. Оно используется для создания различных шифровальных алгоритмов и систем защиты информации.
Одним из самых известных примеров использования деления по модулю в криптографии является RSA-алгоритм. Он использует большие простые числа и математические операции, включая деление по модулю, для генерации секретных ключей и шифрования/дешифрования данных.
Также деление по модулю может быть использовано для проверки целостности данных в хэш-функциях. Хэш-функции преобразуют произвольное сообщение в фиксированный хэш-код определенной длины. При проверке целостности данных, хэш-коды сравниваются с использованием операции деления по модулю для обнаружения изменений в сообщении.
Другим примером использования деления по модулю в криптографии является генерация случайных чисел. Генераторы случайных чисел могут использовать эту операцию для обеспечения равномерного распределения случайных значений в определенном диапазоне.
Таким образом, деление по модулю имеет большое значение в области криптографии и электронной безопасности. Его использование позволяет создавать надежные шифровальные алгоритмы, обеспечивать целостность и проверку данных, а также генерировать случайные числа.
Деление по модулю и вычислительная сложность
При выполнении деления по модулю, компьютер должен выполнить две основные операции: деление и вычисление остатка. Оба этих шага могут быть достаточно ресурсоемкими в зависимости от используемого алгоритма деления и аппаратной реализации системы.
Для выполнения деления по модулю, компьютер должен сначала выполнить обычное деление, как при обычном делении чисел. Затем нужно выполнить операцию вычисления остатка от деления, которая определяет остаток после выполнения обычного деления.
Алгоритмы вычисления остатка от деления могут быть различными, и каждый из них имеет свою вычислительную сложность. Некоторые алгоритмы могут быть более эффективными, чем другие, особенно при больших числах или при работе с определенными типами данных.
Деление по модулю также может быть ресурсоемким при работе с большими числами. Чем больше число, тем больше времени и ресурсов компьютеру потребуется для выполнения деления и вычисления остатка.
Важно учитывать вычислительную сложность деления по модулю, особенно при написании программ, где эффективность работы с числами играет важную роль. Правильный выбор алгоритма и оптимизация кода могут значительно повысить производительность и эффективность вычислительной системы.








