Степенной ряд - это ряд, состоящий из бесконечного числа слагаемых. Каждое слагаемое представляет собой произведение степени переменной на коэффициент. Такой ряд имеет много значений и применений в математике и науке в целом.
Значение степенного ряда заключается в его способности аппроксимировать функции. Он позволяет представить функцию в виде бесконечной суммы мономов, что может быть полезно для анализа их свойств и нахождения приближенных значений. Также степенные ряды часто используются для решения дифференциальных уравнений или изучения поведения функций в окрестности некоторой точки.
Примером степенного ряда может служить ряд Тейлора, который представляет собой разложение функции в бесконечную сумму ее производных в точке разложения. Например, ряд для функции sin(x) в окрестности точки x=0 будет иметь вид: sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
В заключение, степенной ряд - это важный инструмент в анализе функций и решении математических задач. Он позволяет приближенно представить сложные функции в виде бесконечной суммы мономов, что упрощает исследование их свойств и нахождение приближенных значений. Применение степенных рядов широко распространено в различных областях, включая физику, экономику и инженерию.
Что такое степенной ряд? Понятие и основные характеристики
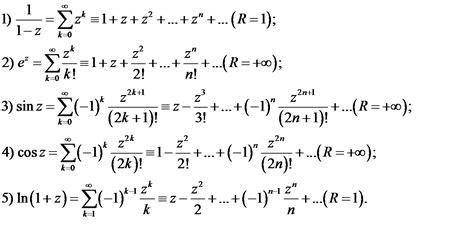
\[ f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + ... + a_nx^n + ... \]
Где \( a_n \) - коэффициенты, которые могут быть любыми числами.
Основной характеристикой степенного ряда является его радиус сходимости. Радиус сходимости - это расстояние от центра степенного ряда (обычно в точке x = 0) до ближайшей точки, в которой ряд сходится. Если ряд сходится во всех точках x, то его радиус сходимости равен бесконечности. Если ряд сходится только в одной точке x, то его радиус сходимости равен нулю.
Степенной ряд может иметь различные функциональные свойства. Он может сходиться или расходиться в зависимости от значения переменной x. В случае сходимости степенной ряд представляет собой бесконечно гладкую функцию, которую можно дифференцировать и интегрировать почленно.
Степенные ряды широко применяются в математическом анализе, теории функций и физике для приближенного представления сложных функций. Они также используются для решения дифференциальных уравнений и моделирования физических процессов.
Определение и сущность степенного ряда
| функция | = | коэффициент0 | + | коэффициент1 * x | + | коэффициент2 * x2 | + | коэффициент3 * x3 | + | ... |
где x - переменная, коэффициенты - постоянные значения, и каждое слагаемое формируется путем возведения x в определенную степень.
Сущность степенного ряда заключается в том, что он позволяет представить сложные функции в виде суммы более простых функций. Такое представление может быть полезным для аппроксимации сложных процессов, приближенного вычисления значений функций в определенной области, а также для решения уравнений и задач математического анализа.
Значение и применение степенных рядов в математике и физике
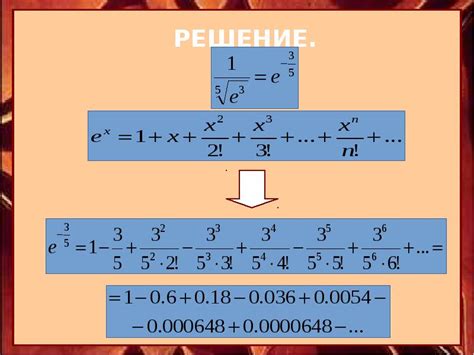
В математике степенные ряды широко используются для аппроксимации функций. Подбором значения коэффициентов можно приближенно представить сложные функции в виде простого выражения. Это позволяет упростить вычисления и проводить аналитические исследования.
В физике степенные ряды применяются для описания реальных процессов и явлений. Например, многие физические законы и уравнения могут быть представлены в виде степенных рядов. Это позволяет сделать модели более точными и учесть множество факторов, влияющих на изучаемое явление.
Примером применения степенных рядов в математике является ряд Тейлора. Он позволяет представить любую функцию, достаточно гладкую и определенную на некотором интервале, в виде бесконечной суммы степенных функций. Ряд Тейлора позволяет получить приближенное значение функции в окрестности заданной точки.
В физике степенные ряды используются для аппроксимации физических законов и решения уравнений. Например, ряд Маклорена является частным случаем ряда Тейлора и применяется для аппроксимации функций приближенно вблизи нуля или других известных точек. Ряды Фурье позволяют разложить сложные колебательные процессы на сумму более простых синусоидальных функций.
- Степенные ряды позволяют аппроксимировать функции в математике и физике.
- Ряд Тейлора позволяет разложить функцию в бесконечную сумму степенных функций.
- Ряд Маклорена является частным случаем ряда Тейлора и применяется приближенно вблизи нуля.
- Ряды Фурье позволяют разложить сложные колебательные процессы на сумму синусоидальных функций.
Примеры степенных рядов и их использование в реальных задачах
1. Ряд Тейлора для экспоненциальной функции
Один из самых известных примеров степенных рядов - это ряд Тейлора для экспоненциальной функции:
ex = 1 + x + x2/2! + x3/3! + ...
Этот ряд позволяет приближенно вычислить значение экспоненты для любого значения x. Он широко используется при решении задач в математике, физике и других науках.
2. Ряд Маклорена для синуса и косинуса
Ещё один важный пример степенных рядов - это ряды Маклорена для синуса и косинуса:
sin(x) = x - x3/3! + x5/5! - x7/7! + ...
cos(x) = 1 - x2/2! + x4/4! - x6/6! + ...
Эти ряды позволяют приближенно вычислить значения синуса и косинуса для любого значения угла x. Они широко используются в многих областях, включая физику, инженерию и компьютерные графики.
3. Ряд Бинома Ньютона
Ещё один пример степенного ряда - это ряд Бинома Ньютона:
(1 + x)n = 1 + nx + n(n-1)x2/2! + n(n-1)(n-2)x3/3! + ...
Этот ряд позволяет приближенно вычислить значение биномиального коэффициента (1 + x)n для любого целого n. Он часто используется в комбинаторике и теории вероятностей.
В заключение, степенные ряды являются мощным инструментом для аппроксимации функций и решения различных задач. Они широко применяются в математике, физике, инженерии, экономике и других науках.








