В геометрии смежные углы играют важную роль и являются одним из основных понятий. Смежными называются углы, которые имеют общую сторону и противоположные стороны расположены на одной прямой. Они представляют собой комбинацию двух углов, которые вместе образуют прямой угол.
Смежные углы обладают несколькими свойствами. Во-первых, сумма смежных углов равна 180 градусам. Иногда это свойство называют «Углы на прямой».
Кроме того, если смежные углы прямые, то они являются смежными прямыми углами. Такие углы равны между собой и образуют равнобедренный прямоугольный треугольник.
Например, прямая угол разделена на два смежных угла. Первый угол составляет 70 градусов, а второй — 110 градусов. Сумма этих углов равна 180 градусам.
Что такое смежные углы и как их определить?
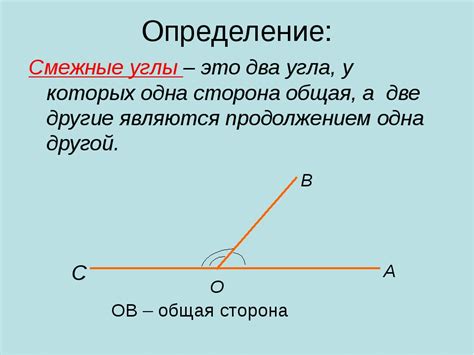
Чтобы определить, являются ли два угла смежными, необходимо проверить, имеют ли они одну общую вершину и общую сторону. Если это так, то углы являются смежными. Например, на рисунке ниже показаны две пары смежных углов:
- Угол AOB и угол COB являются смежными, так как у них есть общая вершина O и общая сторона OB.
- Угол AOC и угол BOC также смежные, так как у них есть общая вершина O и общая сторона OC.
Смежные углы имеют ряд свойств:
- Сумма двух смежных углов всегда равна 180 градусам.
- Если один из смежных углов является прямым, то другой смежный угол также прямой.
- Если две пары смежных углов являются вертикально противоположными, то они равны между собой.
Знание определения и свойств смежных углов позволяет сделать выводы о взаимной зависимости углов и использовать их для решения геометрических задач.
Определение смежных углов
Смежные углы внутри многоугольника получаются, когда стороны двух углов лежат на одной прямой и не прерываются другими сторонами. Это означает, что сумма двух смежных углов будет равна 180 градусам.
 | Смежные углы внутри многоугольника |
Смежные углы при пересечении двух прямых получаются как парные углы, образованные двумя параллельными линиями и прямой, пересекающей их. Вертикальные углы при этом равны, и их сумма также составляет 180 градусов.
 | Смежные углы при пересечении прямых |
Как определить смежные углы на примерах?
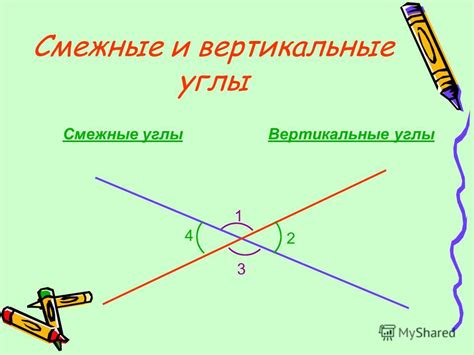
Смежными углами называются два угла, которые имеют общую сторону и общую вершину, но не пересекаются. Для определения смежных углов можно использовать следующие признаки:
- Смотрим на рисунок и находим два угла, которые имеют общую вершину и общую сторону.
- Убеждаемся, что оба угла лежат на одной прямой, то есть сумма их мер равна 180 градусам.
- Проверяем, что эти углы не пересекаются с другими углами на рисунке.
Примеры смежных углов можно найти в различных геометрических фигурах, таких как треугольники, прямоугольники, параллелограммы и трапеции. Например, в треугольнике ABC смежными углами могут быть углы ABD и CBD, так как они имеют общую вершину B и общую сторону AB.
Знание и понимание смежных углов очень полезно при решении задач по геометрии, так как они могут быть использованы для нахождения других углов или доказательства различных свойств геометрических фигур.
Свойства смежных углов
Основные свойства смежных углов:
- Сумма двух смежных углов всегда равна 180 градусов.
- Смежные углы могут быть как смежными дополнительными, так и смежными совместными.
- Смежные углы могут быть вертикальными.
Например, если один из углов равен 60 градусов, то второй угол будет равен 180 минус 60, то есть 120 градусов.
Смежные дополнительные углы дополняют друг друга до 180 градусов. Если один из таких углов равен 30 градусов, то другой угол составит 180 минус 30, то есть 150 градусов.
Смежные совместные углы являются парными углами и дополняют друг друга до 360 градусов. Если один из таких углов равен 60 градусов, то второй угол будет равен 360 минус 60, то есть 300 градусов.
Вертикальные углы – это пара углов, расположенных друг против друга на пересечении двух прямых линий. Такие углы всегда равны друг другу.
Примеры смежных углов:
На рисунке ниже изображены смежные углы ABC и CBD, которые имеют общую сторону BC и вершину B.









