Система неравенств – это набор двух или более неравенств, связанных друг с другом. В отличие от систем уравнений, в системе неравенств необходимо найти такие значения переменных, при которых все неравенства будут выполняться одновременно.
Решение системы неравенств может представлять собой фигуру на координатной плоскости или набор значений, удовлетворяющих всем условиям неравенств. Задачи на решение систем неравенств возникают в различных областях: от математики до экономики и физики.
Для решения систем неравенств используются методы и приемы, аналогичные методам решения систем уравнений. Одним из них является метод подстановки, который заключается в поочередной подстановке найденных значений переменных во все уравнения или неравенства системы. Если все неравенства выполняются, то полученные значения являются решениями системы.
Также для решения систем неравенств применяются методы графического представления и анализа, алгебраические методы, методы сокращенного умножения и другие техники. Часто решение системы неравенств является основой для дальнейшего анализа и принятия решений в различных задачах.
Освоение методов решения систем неравенств позволяет решать сложные задачи, анализировать различные ситуации и прогнозировать развитие событий, основываясь на алгоритмах и логическом мышлении. Эти навыки являются важными как в повседневной жизни, так и в профессиональной деятельности.
Определение системы неравенств

Системы неравенств широко применяются в математике и других науках для моделирования и решения различных задач. Они позволяют найти диапазон возможных значений переменных, удовлетворяющих заданным условиям.
В общем виде систему неравенств можно записать следующим образом:
неравенство 1,
неравенство 2,
... ,
неравенство n.
Где каждое неравенство состоит из левой и правой частей, разделенных знаком неравенства (<, >, ≤, ≥). Левая и правая части могут содержать переменные величины, числа и арифметические операции.
Для решения системы неравенств необходимо найти значения переменных, при которых все неравенства выполняются одновременно. Для этого применяются различные методы, такие как метод подстановки, метод исключения и графический метод.
Примеры систем неравенств
Приведем несколько примеров систем неравенств:
- Система линейных неравенств:
- x + y ≤ 5
- 2x - 3y ≥ -1
- Система квадратичных неравенств:
- x^2 - 4x > 0
- y^2 + 3y ≤ 6
- Система тригонометрических неравенств:
- sin(x)
- cos(x) + 2sin(x) ≥ 1
- Смешанная система неравенств:
- x^2 + y^2
- x + y > 7
- z > -10
Каждая система неравенств может иметь различное количество уравнений и переменных, а также разный вид неравенств. Решать системы неравенств можно различными методами, включая графический, алгебраический, итерационный и др.
Виды систем неравенств

1. Линейные системы неравенств:
Линейные системы неравенств являются одним из самых распространенных видов систем неравенств. Они состоят из нескольких линейных неравенств, в которых неизвестные переменные связаны между собой определенными условиями. Примером линейной системы неравенств может служить система неравенств вида:
2x + 3y > 6
x - y < 4
2. Квадратные системы неравенств:
Квадратные системы неравенств представляют собой системы, в которых присутствуют квадратичные неравенства. Эти системы имеют особую структуру и решаются с использованием специальных методов. Примером квадратной системы неравенств может служить система неравенств вида:
x^2 + y^2 \leq 9
2x - 3y > 0
3. Рациональные системы неравенств:
Рациональные системы неравенств включают в себя неравенства, в которых присутствуют рациональные выражения. Они могут иметь как линейные, так и квадратные неравенства с рациональными коэффициентами. Примером рациональной системы неравенств может служить система неравенств вида:
\frac{x}{2} + \frac{y}{3} \geq 1
\frac{x + y}{x - y} > 0
4. Экспоненциальные системы неравенств:
Экспоненциальные системы неравенств содержат экспоненциальные функции и представляют собой особый класс систем. Решение таких систем требует использования свойств экспоненциальных функций. Примером экспоненциальной системы неравенств может служить система неравенств вида:
2^x - 3^y > 0
e^{x+y} < 1
Каждый вид систем неравенств имеет свои особенности и требует применения специальных методов решения. Правильный выбор метода решения зависит от структуры и типа неравенств, входящих в систему.
Способы решения систем неравенств
Для решения систем неравенств существуют различные методы, которые могут быть использованы в зависимости от условий задачи и количества переменных.
Метод графиков:
Данный метод заключается в построении графиков всех уравнений системы и определении области пересечения графиков, которая и является решением системы неравенств.
Метод подстановки:
Этот метод предполагает подстановку значений переменных из одного уравнения в другие уравнения системы с последующим нахождением допустимых значений переменных, при которых выполняются все условия неравенств.
Метод исключения:
Данный метод заключается в преобразовании системы неравенств с целью исключения одной переменной и последующего решения полученной системы с меньшим количеством переменных.
Метод последовательного включения:
Этот метод предполагает поочередное решение подсистем неравенств, состоящих из двух уравнений, с последующим учетом полученных решений для решения оставшихся уравнений системы.
Метод полного перебора:
Данный метод заключается в исчерпывающем переборе всех возможных значений переменных с проверкой выполнения условий неравенств для каждого набора значений.
Метод линейного программирования:
Этот метод применяется для решения систем линейных неравенств и предполагает определение максимального или минимального значения целевой функции при условии выполнения всех ограничений неравенств.
Выбор метода решения системы неравенств зависит от ее особенностей, количества уравнений и переменных, а также предполагаемого результата.
Метод графического решения системы неравенств
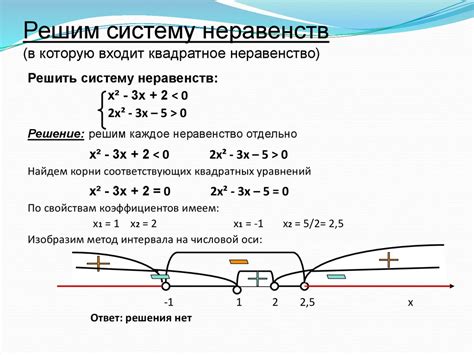
Для начала необходимо построить графики всех уравнений системы на координатной плоскости. Каждому уравнению соответствует прямая или границы области. Затем необходимо определить область пересечения всех этих прямых или область, ограниченную всеми границами неравенств.
Далее, в соответствии с условиями неравенств, необходимо определить, какая часть области пересечения удовлетворяет каждому отдельному неравенству. Для этого используются тестовые точки из каждой области пересечения.
Неравенство, при котором тестовая точка принадлежит области пересечения, является решением системы неравенств. Если тестовая точка не принадлежит области пересечения, нужно проверить следующее неравенство.
Когда все неравенства проверены, решением системы неравенств будет область на плоскости, которая удовлетворяет каждому отдельному неравенству.
Если система неравенств содержит более двух переменных, графическое решение может быть более сложным, так как требует построения многомерных графиков и определения областей пересечения в пространстве.
Метод графического решения системы неравенств является достаточно простым и наглядным способом решения, который позволяет получить визуальное представление множества решений системы.
| Пример системы неравенств | Решение системы неравенств | Графическое представление решения |
|---|---|---|
| 2x + 3y > 6 x - y | x > 1 y |
Метод подстановки для решения системы неравенств
Шаги метода подстановки:
- Выберите одно из уравнений системы и решите его относительно одной из переменных.
- Подставьте найденное значение переменной обратно в остальные уравнения системы.
- Повторяйте шаги 1 и 2, пока не найдете значения всех переменных.
- Проверьте полученные значения, подставив их в исходные неравенства системы, чтобы убедиться, что они удовлетворяют всем условиям.
Пример решения системы неравенств методом подстановки:
Дана система неравенств:
- x + y ≤ 5
- x - y ≥ 1
Решение:
- Выберем первое уравнение и решим его относительно переменной x:
- Подставим найденное значение переменной x во второе уравнение:
- Теперь найдем значение переменной y, подставив найденное значение переменной x в первое уравнение:
- Проверим полученные значения, подставив их в исходные неравенства:
x ≤ 5 - y
(5 - y) - y ≥ 1
5 - 2y ≥ 1
-2y ≥ -4
y ≤ 2
x + 2 ≤ 5
x ≤ 3
3 + 2 ≤ 5 (выполняется)
3 - 2 ≥ 1 (выполняется)
Таким образом, решением данной системы неравенств является x ≤ 3 и y ≤ 2.








