Разрывная функция - это математическая функция, которая не определена в определенной точке или нескольких точках ее области определения. Это означает, что значение функции на этих точках не существует или является бесконечностью. Разрывные функции могут быть интересны исследователям и математикам, так как они позволяют изучать поведение функции в окрестности этих точек и анализировать их свойства.
Свойства разрывных функций могут быть различными, в зависимости от характера разрыва. Различают несколько типов разрывов, включая разрывы первого рода, разрывы второго рода и разрывы третьего рода. Разрыв первого рода наблюдается, когда существуют односторонние пределы функции в разных точках данного интервала. Разрыв второго рода возникает, когда односторонние пределы функции в разных точках интервала являются конечными числами, но значения функции в этих точках отсутствуют. Разрыв третьего рода характеризуется отсутствием пределов функции по обе стороны от точки разрыва.
Примером разрывной функции может служить функция Хевисайда, которая имеет значение 0 при отрицательных аргументах и 1 при положительных аргументах. Эта функция разрывна в точке 0, так как не существует предела функции в этой точке. Другим примером разрывной функции является функция модуля, которая позволяет измерять расстояние между двумя точками на числовой оси. Она разрывна в точке 0, так как значение модуля может быть разное при отрицательных и положительных аргументах.
Что такое разрывная функция
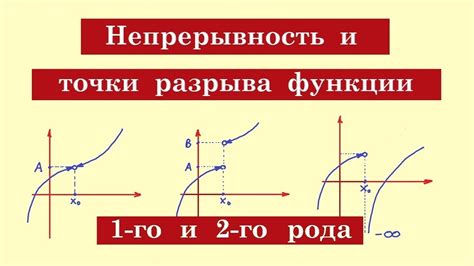
Разрывы функций могут быть различной природы и классифицируются на три основных типа:
- Разрывы первого рода - это точки, в которых функция имеет конечное или бесконечное различие между односторонними пределами. В таких точках функция может иметь различные значения от левой и правой стороны, либо одно значение, но оно не совпадает с левым или правым пределом.
- Разрывы второго рода - это точки, в которых функция имеет скачок или разрыв в значении функции. В таких точках левый и правый пределы могут быть конечными или бесконечными, но функция имеет различные значения от левой и правой стороны.
- Разрывы третьего рода - это точки, в которых функция не имеет предела. В таких точках функция может осциллировать или расходиться в разные стороны.
Примерами разрывных функций могут служить:
- Функция Дирихле, определённая как D(x) = 1, если x - рациональное число, и D(x) = 0, если x - иррациональное число. Эта функция имеет разрывы во всех точках рациональной оси.
- Функция Хевисайда, определённая как H(x) = 0, если x
- Функция знака, определённая как sgn(x) = -1, если x 0. Эта функция имеет разрыв второго рода в точке x = 0.
Разрывные функции играют важную роль в математике и находят применение во многих областях. Изучение их свойств позволяет более глубоко понять поведение функций и решать разнообразные задачи.
Определение и основные свойства
Основные свойства разрывных функций:
- Разрывная функция может иметь различные типы разрывов, включая точечные, разрывы первого рода и разрывы бесконечности.
- Точечный разрыв возникает, когда значение функции меняется в определенной точке, но остается конечным.
- Разрыв первого рода происходит, когда значение функции в некоторой точке стремится к конечному пределу, но само значение функции не существует в этой точке.
- Разрыв бесконечности возникает, когда значение функции стремится к плюс или минус бесконечности в определенной точке.
- Разрывные функции могут быть представлены в виде графиков с прямыми вертикальными или горизонтальными линиями, обозначающими разрывы.
Примеры разрывных функций включают такие функции как ступенчатая функция, функция Дирихле и функция Хэвисайда. Эти функции имеют своеобразные графики и имеют различные типы разрывов в зависимости от своих математических свойств.
Примеры разрывной функции
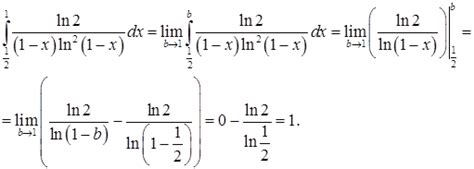
В математике существует множество примеров разрывной функции, которые могут помочь понять ее свойства и особенности. Ниже приведены некоторые из них:
1. Функция Хевисайда:
Функция Хевисайда (или единичная ступенька) определяется следующим образом:
H(x) =
{
0, x
}.
Эта функция имеет скачок значения от 0 до 1 при x = 0.
2. Функция дирихле:
Функция дирихле является примером разрывной функции, определенной как:
D(x) =
{
1, x \in \mathbb{Q}\ 0, x
otin \mathbb{Q}
}.
Эта функция принимает значение 1, если x является рациональным числом, и 0, если x является иррациональным числом.
3. Функция Дирихле-Хевисайда:
Функция Дирихле-Хевисайда комбинирует функции Дирихле и Хевисайда:
DH(x) = H(D(x)).
Эта функция имеет разрыв в каждой точке из множества рациональных чисел.
Эти примеры демонстрируют типичные свойства разрывной функции, такие как изменение значения функции при переходе через точку, а также возможность разрыва на заданных множествах чисел.
Как определить разрывность функции
Основные виды разрывной функции:
1. Разрывы первого рода (устранимые разрывы)
Устранимым разрывом называется такой разрыв, который возникает в результате удаления или замены одной или нескольких точек функции. То есть, если в точке x=a функция имеет значение f(a), а затем значение изменяется на f(b), то в точке x=a будет разрыв первого рода.
2. Разрывы второго рода (разрывы быстрого роста)
Разрывом второго рода называется такой разрыв, в которой функция имеет бесконечное значение (плюс или минус бесконечность) или не имеет предела в данной точке или на бесконечности.
3. Разрывы третьего рода (переносные разрывы)
Переносным разрывом называется такой разрыв, который возникает, когда функция имеет значение более, чем в одной точке, например, в функции Дирихле.
Важно помнить, что непрерывные функции не обязательно являются гладкими и монотонными, а разрывные функции могут иметь различные свойства и формы.
Применение разрывных функций в реальной жизни

Разрывные функции находят применение в различных ситуациях реальной жизни. Например, в экономике разрывные функции используются для описания рыночных процессов. Они могут помочь в моделировании спроса и предложения на товары и услуги и понимании изменений, происходящих на рынке. Разрывные функции также используются в финансовом анализе для оценки рисков и прогнозирования поведения рынка.
В области техники разрывные функции могут применяться, например, для моделирования поведения материалов с неоднородными свойствами. Они могут помочь в анализе различных физических явлений, таких как ломание, изгиб и складывание материалов. Разрывные функции также используются в компьютерной графике и анимации для создания реалистичных эффектов и симуляции различных объектов.
В медицине разрывные функции могут быть использованы для моделирования биологических процессов, таких как сердечные сокращения или нервные импульсы. Они позволяют анализировать и понимать сложные взаимодействия в организме и помогают в разработке новых методов диагностики и лечения. Разрывные функции также могут применяться в психологии, чтобы описывать дискретные изменения в поведении или эмоциональных состояниях.
Таким образом, разрывные функции имеют широкий спектр применения в различных областях и помогают нам лучше понять и анализировать сложные процессы в реальной жизни.








