Парная функция – это математический термин, который применяется для описания отношения между элементами двух разных множеств. Каждый элемент одного множества соответствует ровно одному элементу другого множества. Парная функция может быть задана в виде графа, где каждый элемент одного множества соединен с элементом из другого множества.
Примеры парных функций:
- Для каждого студента в университете может быть задана парная функция, где каждому студенту соответствует его номер зачетки.
- В геометрии парная функция может быть задана для каждой точки на плоскости, где каждой точке соответствует ее координаты (x, y).
- В биологии парная функция может быть задана для каждой особи, где каждой особи соответствует ее генетический код.
Парные функции имеют большое значение в различных областях науки и техники. Они позволяют описывать сложные взаимосвязи между объектами и устанавливать зависимости между ними. Важным свойством парных функций является их однозначность – каждому элементу одного множества соответствует только один элемент другого множества.
Парная функция: определение, примеры, свойства
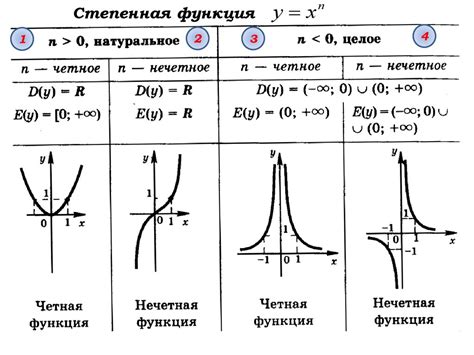
Примером парной функции может быть функция y = 2x, где каждому значению x соответствует значение y, в два раза большее значения x. Например, при x = 1, y = 2, при x = 2, y = 4 и т.д.
Свойства парных функций:
| Свойство | Описание |
|---|---|
| Однозначность | Каждому значению одной переменной соответствует только одно значение другой переменной. |
| Обратимость | Парная функция может быть обратимой, то есть существует функция, обратная парной функции. |
| Инъективность | Если каждому значению одной переменной соответствует разное значение другой переменной, то парная функция является инъективной. |
| Сюръективность | Если каждому значению второй переменной соответствует хотя бы одно значение первой переменной, то парная функция является сюръективной |
| Биективность | Парная функция является биективной, если она одновременно является инъективной и сюръективной. |
Парные функции часто используются для моделирования реальных процессов и явлений, а также в других областях науки и техники.
Что такое парная функция?
В парной функции каждый элемент из области определения называется аргументом, а каждый элемент из области значений называется значением. Областью значений можно считать множество всех значений, которые могут получиться в результате применения парной функции к аргументам из области определения.
Парные функции широко используются в математике, физике, информатике и других областях науки. Они помогают моделировать и описывать реальные ситуации, устанавливать зависимости между различными переменными или объектами. Также парные функции являются основой для понятия графика функции, который отображает связь между аргументами и значениями парной функции.
Примером парной функции может служить функция y = 2x, где x - аргумент, а y - значение. Для каждого значения x можно однозначно определить значение y, умножив x на 2. В данном случае областью определения является множество всех действительных чисел, а областью значений - множество всех действительных чисел, умноженных на 2.
| Аргумент (x) | Значение (y) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
Значение парной функции y = 2x можно представить в виде графика, где на оси абсцисс (по горизонтали) откладываются значения аргументов x, а на оси ординат (по вертикали) откладываются соответствующие значения функции y. В данном случае график будет представлять собой прямую линию, проходящую через начало координат и имеющую угловой коэффициент 2.
Примеры парных функций
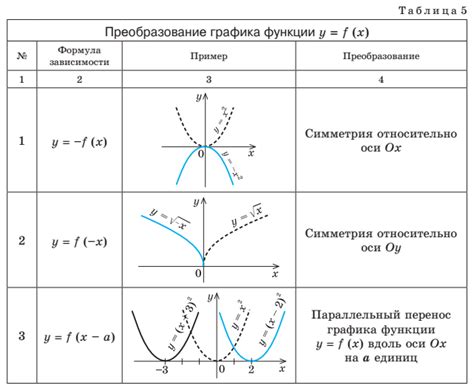
Примером парной функции может служить функция возведения в квадрат. Если у нас есть функция f(x) = x2, то парной функцией будет f-1(x) = √x (читается "корень x"). Возведение в квадрат и извлечение квадратного корня являются взаимообратными операциями.
Еще одним примером парной функции может служить функция нахождения обратного числа. Если у нас есть функция f(x) = 1/x, то парной функцией будет f-1(x) = 1/x. В данном случае парная функция является самой функцией, так как она при повторном применении к результату функции f(x) вернет исходный аргумент.
Также примером парной функции может служить функция нахождения обратной матрицы. Если у нас есть матрица A и ее обратная матрица A-1, то A-1 является парной функцией к матрице A.
Это лишь несколько примеров парных функций, их существует гораздо больше. Парные функции играют важную роль в математике и имеют широкий спектр применений в различных областях науки и техники.
Значение парных функций
Одно из главных преимуществ парных функций состоит в их способности описывать взаимосвязи между входными и выходными значениями. Это позволяет анализировать и предсказывать поведение системы, основываясь на известных данных и моделировать различные сценарии.
Значение парных функций также проявляется в их использовании в криптографии. Одна функция может использоваться для шифрования данных, а другая - для их расшифровки. Это обеспечивает безопасность передаваемой информации и защищает ее от несанкционированного доступа.
Свойства парных функций также играют важную роль в алгоритмах машинного обучения. Используя парные функции, можно оптимизировать процесс обучения модели и улучшить ее точность и эффективность.
В итоге, парные функции имеют огромное значение и применяются в различных областях науки и технологии. Их использование позволяет анализировать данные, моделировать системы и создавать безопасные алгоритмы. Изучение парных функций позволяет лучше понять и улучшить процессы, происходящие в реальном мире.
Свойства парных функций
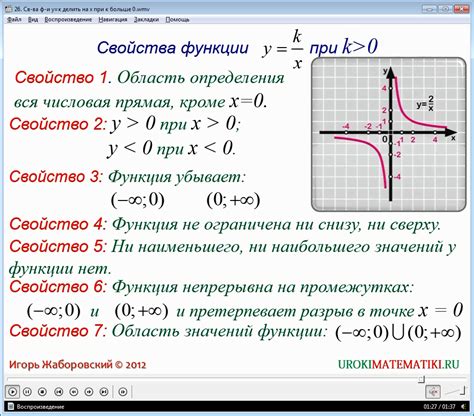
Парные функции обладают рядом важных свойств, которые делают их полезными инструментами в математике и других науках. Вот некоторые из этих свойств:
1. Однозначность: каждому значению аргумента соответствует единственное значение функции. То есть для каждого входного значения существует только одно выходное значение.
2. Взаимная зависимость: парные функции образуют пару так, что если мы знаем значение одной функции, мы можем найти значение другой функции и наоборот. Это свойство позволяет использовать парные функции для решения уравнений и нахождения неизвестных переменных.
3. Симметричность: парные функции обычно имеют симметричные отношения вида (x, y) и (y, x). Имея значение одной функции, мы можем найти значение другой функции, а затем менять их местами, чтобы получить обратные значения.
Пример: парная функция sin(x) и cos(x) обладает всеми указанными свойствами. Зная значение sin(x), мы можем использовать связь sin^2(x) + cos^2(x) = 1, чтобы найти значение cos(x) и наоборот.
Важно отметить, что не все функции являются парными функциями. Для того, чтобы функции были парными, они должны обладать вышеуказанными свойствами.
Как определить парную функцию?
- Каждому элементу доминанты соответствует ровно один элемент кодоминанты.
- Ни одному элементу доминанты не соответствует более одного элемента кодоминанты.
Для более наглядного понимания концепции парных функций, рассмотрим примеры:
Пример 1:
Доминанта: {1, 2, 3}
Кодоминанта: {a, b, c}
Парная функция: {(1, a), (2, b), (3, c)}
Пример 2:
Доминанта: {1, 2, 3}
Кодоминанта: {a, b}
Парная функция: {(1, a), (2, b), (3, b)}
Парные функции имеют важное значение в математике и информатике, поскольку они позволяют установить однозначное соответствие между элементами двух множеств. Это делает их полезными для моделирования связей и отношений в различных областях знаний.
Свойства парных функций включают:
- Инъективность: каждый элемент доминанты соответствует различному элементу кодоминанты.
- Сюръективность: каждый элемент кодоминанты имеет соответствующий элемент в доминанте.
- Биективность: функция является и инъективной, и сюръективной, то есть выполняются оба условия.
Таким образом, определение парной функции сводится к тому, чтобы убедиться, что каждому элементу доминанты соответствует ровно один элемент кодоминанты, и ни одному элементу доминанты не соответствует более одного элемента кодоминанты.
Применение парных функций
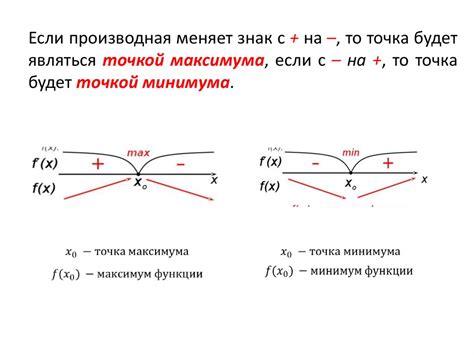
Парные функции имеют широкое применение в различных областях, включая математику, физику, экономику и информатику. Ниже приведены некоторые примеры использования парных функций:
1. Графическое представление данных: Парные функции могут быть использованы для графического представления данных. Например, парная функция может быть использована для построения графика зависимости температуры от времени.
2. Решение уравнений: Парные функции могут помочь в решении уравнений. Например, парная функция может быть использована для нахождения корней квадратного уравнения.
3. Моделирование систем: Парные функции могут быть использованы для моделирования различных систем. Например, парная функция может быть использована для описания движения тела в физике.
4. Оптимизация: Парные функции могут быть использованы для оптимизации процессов или систем. Например, парная функция может быть использована для поиска наилучшего решения задачи.
5. Криптография: Парные функции могут быть использованы в криптографии для шифрования и дешифрования данных. Например, парные функции могут быть использованы для создания цифровой подписи.
Применение парных функций в различных областях позволяет решать сложные задачи и упрощать процессы. Наличие парной функции важно для анализа, моделирования и определения зависимостей между переменными.
Взаимосвязь парных функций и графиков
График парной функции представляет собой множество точек на плоскости, где каждой точке соответствует значение входных и выходных переменных функции. Графики парных функций могут быть представлены в виде таблицы, графика или векторной диаграммы.
Анализ графиков парных функций позволяет выявить различные типы зависимостей между переменными, такие как линейные, нелинейные или случайно-распределенные зависимости. Например, линейная зависимость может быть представлена прямой линией на графике, а нелинейная зависимость - кривой или поверхностью.
Взаимосвязь парных функций и графиков является важным инструментом для анализа и моделирования сложных систем, таких как физические процессы, экономические модели, социальные взаимодействия и т. д. Парные функции и их графики позволяют наглядно представить и изучить изменения в различных переменных и их взаимосвязь.
Кроме того, парные функции и графики могут быть использованы для решения математических задач, таких как оптимизация, поиск экстремумов, определение равновесных состояний, и т. д. Анализ графиков парных функций помогает выявить особенности существующих зависимостей и предсказать поведение системы при изменении параметров.
Как использовать парные функции в программировании?

Одним из примеров парных функций является функция "add" и "subtract". Функция "add" складывает два числа, а функция "subtract" вычитает одно число из другого. Обе функции могут использовать один и тот же набор аргументов (например, два числа), но выполняют противоположные действия.
Использование парных функций помогает упростить и улучшить структуру кода. Вместо того, чтобы создавать две отдельные функции для каждого действия, можно использовать одну парную функцию. Это уменьшает количество кода и делает его более логичным и понятным.
Парные функции также помогают повысить повторное использование кода. Если у вас есть две функции, которые выполняют противоположные действия, вы можете использовать одну функцию вместо другой в разных частях программы, в зависимости от необходимости.
С помощью парных функций легко выполнять операции чтения и записи данных. Например, если вы создаете функцию "readFile" для чтения данных из файла, вы можете создать парную функцию "writeFile", которая будет записывать данные в файл. Это делает работу с файлами более удобной и интуитивно понятной.
Одним из примеров парных функций в языке программирования JavaScript является функция "parseInt" и "toString". Функция "parseInt" преобразует строку в число, а функция "toString" преобразует число в строку. Они являются противоположными операциями, но могут использовать одни и те же аргументы.
В заключение, парные функции предоставляют удобный и гибкий способ организации кода. Они помогают упростить его структуру, повысить читаемость и повторно использовать код. Использование парных функций является хорошей практикой в программировании и помогает создавать более эффективные и понятные программы.








