Оценка интеграла является важной задачей в математике и науке в целом. Оно позволяет вычислить значение определенного интеграла на заданном интервале, что имеет большое практическое значение в различных областях знаний. Понимание этого понятия и владение методами оценки интеграла необходимо для успешного решения множества задач, связанных с анализом функций и вычислением площадей, объемов и других величин.
Существует несколько методов оценки интегралов, которые используются в зависимости от конкретной задачи и условий. Один из наиболее распространенных методов - прямоугольное разбиение. Он заключается в разбиении интервала, на котором задана функция, на равные промежутки и вычислении площади прямоугольников, образованных этим разбиением. Другой метод, частичные суммы, основан на приближенном вычислении значения интеграла с помощью суммы значений функции на равноотстоящих точках разбиения.
Точность оценки интеграла зависит от выбранного метода и способа разбиения интервала. Чем меньше промежутки, на которые разбивается интервал, тем более точная будет оценка, однако при этом возрастает вычислительная сложность задачи. Поэтому при выборе метода оценки интеграла необходимо учитывать как требования к точности результата, так и ресурсы, доступные для вычисления.
Оценка интеграла
Оценка интеграла основывается на разбиении интервала интегрирования на малые отрезки и аппроксимации функции на каждом отрезке. Наиболее распространенными методами оценки интеграла являются методы прямоугольников, тrapezoid rule, Simpson's rule и метод Монте-Карло.
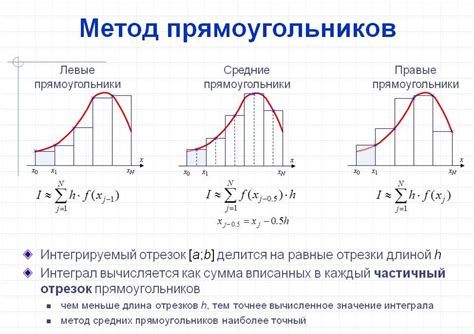
Метод прямоугольников основан на аппроксимации функции на каждом отрезке некоторым постоянным значением. Интеграл вычисляется как сумма площадей прямоугольников, которые охватывают график функции.
Метод трапеции подразумевает аппроксимацию функции на каждом отрезке линейной функцией, образующейся соединением двух соседних точек графика. Интеграл вычисляется как сумма площадей трапеций, образованных графиком функции и осью x.
Метод Симпсона представляет функцию на каждом отрезке параболой, проходящей через три точки графика функции. Интеграл вычисляется как сумма площадей парабол, охватывающих график функции.
Метод Монте-Карло использует случайные числа для оценки интеграла. Интеграл вычисляется путем генерации случайных точек внутри интервала интегрирования и подсчета доли точек, попавших под график функции.
Выбор метода оценки интеграла зависит от характеристик функции и требуемой точности. Каждый метод имеет свои преимущества и ограничения, и его выбор может быть обусловлен конкретной задачей или доступными вычислительными ресурсами.
Понятие интеграла
Интеграл определяется как предел суммы площадей бесконечного числа бесконечно малых прямоугольников, образующих площадь под кривой.
Интеграл может быть определен как неопределенный или определенный. Неопределенный интеграл позволяет найти антипроизводную функции, то есть функцию, производная которой равна данной функции. Определенный интеграл вычисляет точное значение площади под кривой на заданном интервале.
Интегралы находят широкое применение в различных областях науки и техники. Они являются одним из основных инструментов в математическом моделировании и численных методах решения дифференциальных уравнений.
Одним из основных методов вычисления интегралов является метод Ньютона-Лейбница, который основан на использовании основного свойства интеграла – аддитивности, а также на использовании таблиц интегралов и специальных методов интегрирования.
Таким образом, понятие интеграла играет важнейшую роль в математическом анализе и имеет широкое применение в различных областях науки и техники. Оно позволяет вычислять площади под кривыми, решать задачи нахождения среднего значения и длины кривой, а также является основой для численных методов решения дифференциальных уравнений.
Методы оценки интеграла

Одним из основных методов оценки интеграла является метод прямоугольников. При этом методе, область под графиком функции на отрезке разбивается на прямоугольники, и значение интеграла на каждом прямоугольнике приближенно равно произведению длины прямоугольника на значение функции в одной из его точек. Сумма таких произведений для всех прямоугольников дает приближенное значение интеграла.
Другим часто используемым методом является метод тrapezoid, он основан на аппроксимации графика функции отрезками прямых. При этом методе, область под графиком функции на отрезке разбивается на трапеции, и значение интеграла на каждой трапеции приближенно равно произведению полусуммы высоты трапеции и суммы длины ее оснований. Сумма таких произведений для всех трапеций дает приближенное значение интеграла.
Еще одним методом оценки интеграла является метод парабол (метод Симпсона). При этом методе, область под графиком функции на отрезке разбивается на параболы, и значение интеграла на каждой параболе приближенно равно произведению третью часть суммы значений функции в начальной, конечной и средней точках параболы, умноженной на шаг интегрирования. Сумма таких произведений для всех парабол дает приближенное значение интеграла.
Каждый из этих методов имеет свои плюсы и минусы, и выбор конкретного метода зависит от особенностей задачи и требуемой точности оценки интеграла. При использовании данных методов следует также учитывать особенности функции, ее гладкость и свойства на заданном отрезке.
| Метод | Принцип | Преимущества | Недостатки |
|---|---|---|---|
| Метод прямоугольников | Разбиение области на прямоугольники | Простая реализация, хорошо подходит для большого числа прямоугольников | Малая точность при разбиении на небольшое число прямоугольников |
| Метод трапеций | Разбиение области на трапеции | Более точная аппроксимация графика функции | Меньшая точность при разбиении на неравномерные трапеции |
| Метод парабол (Симпсона) | Разбиение области на параболы | Высокая точность, особенно при использовании большого числа парабол | Сложная реализация, недостаточно эффективен для функций сложной формы |








