Итерационный метод - это математический алгоритм, который применяется для приближенного решения сложных задач. Он основан на принципе последовательного повторения одной и той же операции над начальным значением, чтобы получить все более точные результаты.
Итерационный метод может быть использован для решения различных задач, включая численное интегрирование, приближенное нахождение корней уравнений и оптимизацию функций. Он позволяет приблизиться к истинному значению решения, шаг за шагом, с учетом ошибок, до достижения заданной точности.
Ключевой компонент итерационного метода - это итерация. При каждой итерации промежуточный результат используется в качестве входных данных для следующей итерации, что позволяет наращивать точность решения.
Принцип работы итерационного метода достаточно прост. Сначала задается начальное значение, которое выбирается произвольно или на основе определенных условий задачи. Затем выполняется серия итераций, где каждая итерация состоит в применении определенной функции или операции к предыдущему результату.
Определение итерационного метода

Основной принцип итерационного метода состоит в следующем:
- Задается исходное приближение решения.
- Применяется итерационная формула или алгоритм, который позволяет перейти от предыдущего приближения к новому.
- Полученное новое приближение сравнивается с требуемой точностью. Если точность не достигнута, возвращаются ко второму пункту.
В процессе итерационного метода каждая итерация приближает решение к истинному значению. Количество требуемых итераций зависит от точности, которую необходимо достичь, а также от свойств задачи и выбранного итерационного метода.
Итерационные методы широко применяются в различных областях науки и техники, таких как математика, физика, компьютерные науки и другие. Они позволяют решать сложные задачи, для которых не существует аналитического решения или аналитическое решение слишком сложно или затруднительно.
Одним из примеров итерационного метода является метод простой итерации для решения уравнений вида f(x) = 0. Другим примером является метод Гаусса-Зейделя для решения систем линейных уравнений.
| Преимущества | Недостатки |
|
|
Основные принципы итерационного метода
Основные принципы итерационного метода включают в себя:
| 1. Инициализация | Начальное приближение к решению задачи устанавливается на первом шаге метода. Это может быть произвольное значение или значение, полученное из предыдущих вычислений. |
| 2. Итерации | Итерации представляют собой повторение одной и той же операции с использованием текущего значения приближения. На каждом шаге итерации выполняются математические вычисления или другие операции, приводящие к уточнению значения решения. |
| 3. Остановка | Остановка происходит, когда достигнута необходимая точность или выполнено установленное количество итераций. Решение, полученное после остановки, считается приблизительным или окончательным решением задачи. |
| 4. Проверка сходимости | Перед началом итерационного метода необходимо проверить, сходится ли метод для данной задачи и начального приближения. Если метод не сходится, то может потребоваться изменение начального приближения или выбор другого метода. |
| 5. Выбор функции итерации | Выбор функции итерации играет важную роль в эффективности и сходимости итерационного метода. Хорошо выбранная функция итерации должна приводить к ускорению сходимости или увеличению точности решения. |
Основные принципы итерационного метода позволяют эффективно решать широкий спектр задач в различных областях науки и техники. Итерационный метод применяется в алгебре, математическом анализе, оптимизации, численных методах, физике, экономике и многих других областях, где требуется точное или приближенное решение задачи.
Роль итерационного метода в решении задач

Итерационный метод играет важную роль в решении различных задач, особенно в научных и инженерных областях. Этот метод используется для приближенного решения уравнений и систем уравнений, задач оптимизации и других математических задач.
Идея итерационного метода заключается в последовательном приближении к точному решению путем повторяющегося применения заданной процедуры или формулы. Каждая итерация (повторение) приближает решение к искомому значению с заданной точностью.
Одним из наиболее распространенных примеров применения итерационного метода является нахождение корня уравнения. Для этого выбирается начальное приближение и повторяются итерации, пока не будет достигнута достаточная точность. Такой метод часто используется для решения нелинейных уравнений, где аналитическое решение отсутствует или сложно получить.
Кроме того, итерационные методы активно применяются в задачах оптимизации, где требуется найти максимум или минимум некоторой функции. В таких задачах итерационный метод позволяет последовательно улучшать текущее приближение, пока не будет достигнут оптимальный результат.
Итерационные методы также широко используются в численных моделях и симуляциях. В таких случаях существует необходимость в пошаговом приближенном решении сложных математических моделей, которые могут быть слишком сложными или затратными для решения аналитическими методами.
В целом, итерационный метод предоставляет простой и эффективный способ приближенного решения различных задач. Он позволяет достичь нужной точности с помощью последовательных шагов, обеспечивая удобство и гибкость в процессе решения задачи.
Алгоритм итерационного метода
Алгоритм итерационного метода обычно включает в себя следующие шаги:
- Выбрать начальное приближение к решению задачи.
- Провести итерацию, используя выбранное начальное приближение.
- Проверить достижение условия остановки.
- Если достигнуто, завершить итерационный процесс и вернуть найденное приближенное решение.
- Если условие остановки не выполнено, вернуться к шагу 2 и продолжить итерацию.
Каждая итерация выполняется путем обновления текущего приближения с использованием определенной формулы или алгоритма. Этот процесс повторяется до тех пор, пока не будут выполнены условия остановки.
Итерационные методы часто используются в различных областях науки и инженерии, таких как математика, физика, экономика и многое другое. Они позволяют найти приближенные решения сложных задач, когда точное аналитическое решение является невозможным или очень сложным для вычисления.
Шаги выполнения итерационного метода
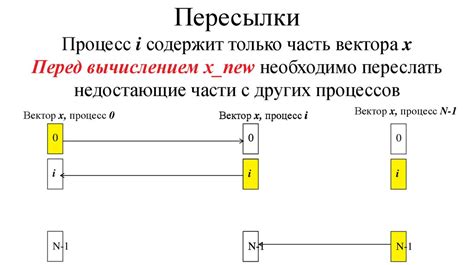
Шаги выполнения итерационного метода обычно выглядят следующим образом:
- Выбор начального приближения.
- Выполнение итерационной формулы до достижения заданной точности или удовлетворения заданному критерию остановки.
- Проверка достижения заданной точности или удовлетворения критерию остановки.
- Если точность не достигнута или критерий остановки не выполнен, переход к следующей итерации.
- Если точность достигнута или критерий остановки выполнен, вывод результата.
На каждом шаге выполнения итерационного метода происходит повторение одной и той же операции – вычисление нового значения на основе предыдущего значения. Этот процесс повторяется до достижения необходимой точности или выполнения заданного критерия остановки.
| Шаг | Действие |
|---|---|
| 1 | Выбор начального приближения |
| 2 | Выполнение итерационной формулы |
| 3 | Проверка достижения точности или критерия остановки |
| 4 | Переход к следующей итерации |
| 5 | Вывод результата |
Итерационные методы широко применяются в различных областях науки и техники для решения сложных математических задач. Благодаря своей простоте и эффективности, итерационные методы стали неотъемлемой частью алгоритмов численного анализа и нахождения приближенных решений.
Пример применения итерационного метода
В качестве примера рассмотрим уравнение f(x) = x^2 - 4. Мы знаем, что корни этого уравнения равны x1 = -2 и x2 = 2.
Начнем с некоторого начального приближения x0. Для уравнения f(x) = x^2 - 4 можно выбрать, например, x0 = 1.
Последовательно вычисляем значения $x_{n+1} = f(x_n)$ до тех пор, пока $\| x_{n+1} - x_n \| > \epsilon$, где $\epsilon$ – некоторая малая положительная величина, задающая точность вычисления.
В нашем случае, после нескольких итераций, мы получаем следующую последовательность приближений: x0 = 1, x1 = 3, x2 = -5, x3 = 21, x4 = 439, ... Наблюдаем, что значения последовательности расходятся, так как величина $| x_{n+1} - x_n |$ не стремится к нулю.
Чтобы избежать расходимости, можно воспользоваться другим итерационным методом, например, методом Ньютона. В этом случае, при правильном выборе начального приближения x0, последовательность значений будет сходиться к искомому корню.
Таким образом, итерационный метод может использоваться для решения различных задач, включая поиск корня уравнения. Он позволяет приближенно вычислять значения функций, оптимизировать параметры моделей и решать другие задачи математического анализа. Для каждой конкретной задачи необходимо выбирать подходящий итерационный метод и правильное начальное приближение.
Виды итерационных методов
Существует несколько видов итерационных методов, которые применяются для решения различных задач. Рассмотрим некоторые из них:
| Название | Описание |
|---|---|
| Метод простой итерации | Данный метод основывается на построении последовательности приближений, которая сходится к искомому решению. Он выполняет итеративные шаги до достижения заданной точности или определенного числа итераций. |
| Метод Ньютона | Метод Ньютона является более эффективным итерационным методом, который используется для численного решения нелинейных уравнений. Он основывается на линейной аппроксимации функции и поиске корней с использованием ее производной. |
| Метод последовательных приближений | Этот метод применяется для нахождения приближенного решения интегрального уравнения. Он заключается в построении последовательности приближений, которая сходится к решению. Каждое новое приближение вычисляется на основе предыдущего. |
| Метод Якоби | Метод Якоби применяется для решения систем линейных алгебраических уравнений. Он основывается на разложении матрицы системы на диагональную и остаточную, а затем выполняет итеративные шаги для приближенного решения. |
Каждый из этих методов имеет свои преимущества и недостатки, и их выбор зависит от конкретной задачи, которую необходимо решить. Важно учитывать особенности задачи и требования к точности результата при выборе итерационного метода.
Метод простой итерации
Идея метода простой итерации заключается в следующем:
- Исходная задача приводится к виду x = Ф(x), где Ф(x) - некоторая функция, которая полностью определяет задачу.
- Выбирается начальное приближение x0.
- Вычисляется следующее приближение x1 = Ф(x0).
- Процесс повторяется до достижения заданной точности или до выполнения другого критерия остановки.
Сходимость метода простой итерации зависит от выбора функции Ф(x). Часто используется линейная функция, тогда итерационный процесс записывается в виде xn+1 = a·xn + b, где a и b - некоторые константы.
При правильном выборе параметров метод простой итерации сходится к решению задачи. Однако нужно быть осторожным, так как некорректный выбор функции или начального приближения может привести к расходимости или к сходимости к некорректному решению.
Метод Ньютона

Основная идея метода Ньютона заключается в последовательном приближении к искомому корню путем линеаризации функции вблизи начального приближения. Алгоритм метода состоит из нескольких итераций, на каждой из которых выполняются следующие шаги:
- Выбирается начальное приближение.
- На каждой итерации вычисляется значение функции и ее производной в текущей точке.
- Вычисляется приближение к следующей точке с помощью формулы: xn+1 = xn - f(xn)/f'(xn), где f(xn) - значение функции в текущей точке, f'(xn) - значение производной функции в текущей точке.
- Повторяются шаги 2-3 до достижения заданной точности или заданного числа итераций.
Метод Ньютона сходится очень быстро при достаточно хорошем начальном приближении и гладкой функции. Однако, на практике может возникнуть ряд проблем, таких как выбор плохого начального приближения или возможные особые точки исследуемой функции.
В целом, метод Ньютона является эффективным и надежным инструментом для численного решения уравнений, но его применение требует некоторого опыта и внимания к особенностям изучаемой функции.
Метод Гаусса-Зейделя
Основная идея метода Гаусса-Зейделя заключается в последовательном пересчете компонентов вектора неизвестных, пока не будет достигнуто требуемое значение точности. В отличие от метода итераций, где все компоненты вектора вычисляются одновременно, метод Гаусса-Зейделя пересчитывает их последовательно, используя уже полученные значения.
Алгоритм метода Гаусса-Зейделя выглядит следующим образом:
- Устанавливаем начальное приближение для вектора неизвестных.
- Повторяем следующие шаги до достижения требуемой точности:
- Для каждого уравнения системы:
- Вычисляем сумму произведений коэффициентов уравнения на соответствующие компоненты вектора неизвестных, кроме текущего.
- Вычитаем полученную сумму из правой части уравнения.
- Делим полученное значение на коэффициент при текущем компоненте вектора неизвестных.
- Обновляем значение текущей компоненты вектора неизвестных.
- Для каждого уравнения системы:
Метод Гаусса-Зейделя обычно сходится быстрее, чем метод итераций, если матрица системы является диагонально приближенной. Однако для некоторых систем может потребоваться большое количество итераций для достижения требуемой точности.








