Дифференцированная функция представляет собой математическую концепцию, которая используется для определения скорости изменения функции в каждой ее точке. В общем случае, она представляет собой производную от функции и является одним из основных инструментов дифференциального исчисления. Определение дифференцированной функции дает возможность получить множество полезных сведений о поведении функции и ее экстремальных точках, что делает ее необходимым инструментом в различных областях науки и инженерии.
Дифференцированные функции активно используются в физике, экономике, информатике и других областях для моделирования и анализа реальных процессов. Они позволяют определить мгновенные скорости изменения величин, например, скорость движения объекта или изменение стоимости товара в зависимости от времени. Кроме того, дифференцированная функция позволяет изучать экстремальные точки функции, такие как минимумы и максимумы, что находит применение в оптимизации задач и нахождении оптимальных решений.
Примером использования дифференцированной функции может быть расчет скорости свободного падения объекта или нахождение оптимального времени для доставки груза в условиях ограниченной скорости и ресурсов.
Использование дифференцированной функции требует навыков работы с дифференциальным исчислением и математическим анализом. Однако, основные концепции можно усвоить и применить в реальных задачах, что делает дифференцированную функцию полезным инструментом для анализа различных процессов и явлений.
Определение дифференцированной функции

Формально, функция \(f(x)\) называется дифференцированной в точке \(x_0\), если существует предел:
\[f'(x_0) = \lim_{x \to x_0} \frac{{f(x) - f(x_0)}}{{x - x_0}}\]
Если предел существует, то его значение называется производной функции \(f(x)\) в точке \(x_0\).
Производная функции является основным понятием математического анализа и имеет широкий спектр применений. Например, она позволяет найти экстремумы функции (максимумы и минимумы), определить изменение направления функции (растет или убывает), а также решать задачи из различных научных и технических областей.
Производная функции: определение и свойства
Производная функции обозначается как f'(x) или dy/dx. Она представляет собой предел отношения приращения значения функции к приращению аргумента при его бесконечном уменьшении или увеличении:
f'(x) = lim(h→0) (f(x+h) - f(x)) / h
Существует несколько свойств производной функции, которые помогают анализировать ее поведение:
- Если производная функции положительна в точке x, то значение функции возрастает в этой точке.
- Если производная функции отрицательна в точке x, то значение функции убывает в этой точке.
- Если производная функции равна нулю в точке x, то в этой точке функция имеет экстремум (минимум или максимум).
- Если производная функции изменяет знак с плюса на минус в точке x, то в этой точке функция имеет локальный максимум.
- Если производная функции изменяет знак с минуса на плюс в точке x, то в этой точке функция имеет локальный минимум.
Производная функции позволяет решать множество задач, связанных с оптимизацией, моделированием, физикой и другими областями. Она позволяет оптимизировать процессы, находить точки экстремума функции, а также анализировать ее поведение в различных точках. Использование производной функции является неотъемлемой частью дифференциального исчисления и имеет широкое применение в различных областях знания.
Производная функции: геометрическая интерпретация

Геометрический смысл производной заключается в том, что она представляет собой тангенс угла наклона касательной к графику функции в каждой ее точке. Если взять две близкие точки на графике функции и провести через них прямую, то ее наклон будет приближенно равен значению производной в данной точке.
Например, если производная функции положительна в данной точке, это означает, что график функции в этой точке наклонен вверх, а если производная отрицательна, то график функции наклонен вниз. Если же производная равна нулю, то это указывает на наличие экстремума в данной точке.
Для наглядного представления геометрического смысла производной можно построить таблицу значений, содержащую значения функции и ее производной в различных точках. Затем на основе этих данных можно построить график функции и касательные к нему в каждой точке. Это позволяет визуально представить изменение угла наклона касательных и его связь с производной функции.
| Значение x | Значение функции f(x) | Значение производной f'(x) |
|---|---|---|
| x1 | f(x1) | f'(x1) |
| x2 | f(x2) | f'(x2) |
| x3 | f(x3) | f'(x3) |
Построение такой таблицы и графика функции позволяет наглядно увидеть и проанализировать геометрический смысл производной – угол наклона касательной к графику функции в каждой ее точке.
Алгебраические и тригонометрические функции: примеры использования дифференцирования
Алгебраические функции:
Дифференцирование алгебраических функций позволяет находить производные и изучать их свойства. Например, при анализе зависимости пути от времени при движении объекта можно использовать дифференцирование алгебраической функции. При этом производная будет описывать скорость изменения пути, а показательная функция будет применяться, чтобы найти функцию пути от времени.
Пример 1:
Рассмотрим функцию f(x) = x^2, которая описывает площадь квадрата в зависимости от стороны. Дифференцирование этой функции позволяет найти производную f'(x) = 2x. Таким образом, мы можем узнать, как изменяется площадь квадрата при изменении стороны.
Пример 2:
Рассмотрим линейную функцию f(x) = mx + b, где m – угловой коэффициент, b – свободный член. Дифференцируя эту функцию, мы получим производную f'(x) = m, которая будет равна угловому коэффициенту. Таким образом, дифференцирование линейной функции позволяет найти значение углового коэффициента, что может быть полезно при анализе графика.
Тригонометрические функции:
Дифференцирование тригонометрических функций позволяет находить производные и изучать их свойства. Оно применяется, например, при вычислении скоростей, углов и изменений величин при колебаниях и вращениях.
Пример 1:
Рассмотрим функцию f(x) = sin(x), которая описывает зависимость синуса от аргумента. Дифференцирование этой функции позволяет найти производную f'(x) = cos(x), которая будет равна косинусу. Таким образом, мы можем узнать, как изменяется значение синуса при изменении аргумента.
Пример 2:
Рассмотрим функцию f(x) = tan(x), которая описывает зависимость тангенса от аргумента. Дифференцируя эту функцию, мы получим производную f'(x) = sec^2(x), где sec(x) – секанс. Таким образом, дифференцирование позволяет найти значение секанса и изучать свойства функции тангенса.
Функции нескольких переменных: дифференцирование по нескольким переменным
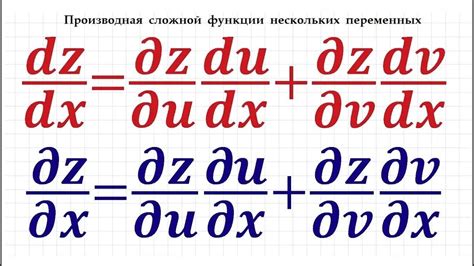
Когда мы говорим о дифференцировании функции, обычно предполагаем, что функция зависит только от одной переменной. Однако в некоторых случаях функции могут зависеть от нескольких переменных одновременно.
Дифференцирование функций нескольких переменных происходит аналогично дифференцированию функций одной переменной, только теперь мы учитываем все переменные, по которым функция зависит.
Пусть у нас есть функция f(x, y, z), зависящая от трех переменных. Чтобы дифференцировать эту функцию, нужно взять частные производные по каждой переменной. Например, чтобы найти частную производную функции f(x, y, z) по переменной x, необходимо зафиксировать остальные переменные (y и z) и дифференцировать функцию относительно x как обычную функцию одной переменной.
Другими словами, дифференцирование функции нескольких переменных – это процесс нахождения изменения функции при изменении каждой переменной отдельно, при условии, что все остальные переменные остаются постоянными.
Дифференцирование функций нескольких переменных имеет множество применений в различных областях, таких как физика, экономика, инженерия и математика. Например, в экономике дифференцирование функции нескольких переменных может быть использовано для определения эластичности спроса на товары при изменении цены и дохода.
Примеры использования дифференцирования в физике и экономике
В физике применение дифференцирования широко распространено. Одним из примеров использования дифференциального исчисления является рассмотрение движения тела, когда зная зависимость координаты от времени, можно вычислить скорость движения и ускорение тела. Дифференцирование также позволяет анализировать графики функций, определяющих законы движения, и находить экстремумы, такие как точки максимума и минимума дальности полета снаряда или максимальная скорость движения свободного падения.
В экономике дифференцирование используется для изучения изменений в экономических показателях, таких как спрос, предложение, доходы и расходы, чтобы определить их тенденции и принять соответствующие меры. Например, дифференцирование помогает анализировать зависимость между спросом на товар и его ценой, а также определять эластичность спроса, то есть изменение спроса в ответ на изменение цены. Дифференцирование также позволяет исследовать издержки производства и определить оптимальный уровень производства и цену, максимизирующие прибыль.
В обоих случаях дифференцирование является мощным инструментом анализа, который позволяет получить более точные и детальные данные и сделать более обоснованные выводы о характеристиках объектов и процессов в физике и экономике.
Сходимость и сравнение функций: применение дифференцирования в математическом анализе

Сходимость функции показывает, как функция приближается к определенной точке или значению при изменении аргумента. Дифференцирование позволяет исследовать эту сходимость, а именно выяснить, насколько быстро функция приближается к заданной точке. Например, при исследовании ряда можно использовать дифференцирование для определения его сходимости к определенному пределу.
Сравнение функций также является важным инструментом в математическом анализе. Дифференцирование позволяет сравнивать функции между собой и выяснить, какая функция растет быстрее или медленнее другой в определенном интервале.
Например, пусть у нас есть две функции: f(x) и g(x). Если мы дифференцируем обе функции и сравниваем их производные, то можем определить, в каких точках f(x) растет быстрее, а в каких - медленнее, чем g(x). Это может быть полезно при анализе экономических данных, например, при сравнении темпов роста двух разных компаний.
Дифференцирование также позволяет анализировать экстремумы функций. Если мы находим точки, в которых производная функции равна нулю или не существует, то это могут быть точки максимума или минимума функции. Это позволяет найти точки перегиба и экстремальные значения функции.
Таким образом, дифференцирование играет важную роль в исследовании сходимости и сравнения функций в математическом анализе. Оно позволяет определить, как функция приближается к определенным значениям и как она сравнивается с другими функциями. Эти знания могут быть полезными в различных областях науки и применяются для изучения различных явлений и процессов.








