Когда мы говорим о функции, важно понимать значение нулями функции. Определение этого понятия связано с понятием нулей функции - значения аргумента, при которых функция равна нулю. Точки, в которых функция обращается в ноль, играют важную роль в анализе и изучении функций.
Понятие нулями функции позволяет нам понять поведение функции и ее особенности. Например, нулями могут быть стационарные точки функции, экстремумы или корни уравнений, которые функция удовлетворяет. Значение нулями функции помогает нам определить интервалы, на которых функция положительна или отрицательна, и понять, как она меняет свое поведение.
Рассмотрим пример для наглядного понимания значения нулями функции. Рассмотрим функцию f(x) = x^2 - 4. Чтобы найти нули этой функции, мы должны найти значения x, при которых функция равна нулю. Уравнение x^2 - 4 = 0 приводит к решению x = ±2. То есть, нули функции f(x) = x^2 - 4 равны -2 и 2.
Значение нулями функции играет важную роль в математическом анализе. Оно помогает нам понять поведение функций и их особенности. Понимание значения нулями функции позволяет нам решать уравнения, определить интервалы изменения функции и изучить ее характеристики.
Определение нулей функции
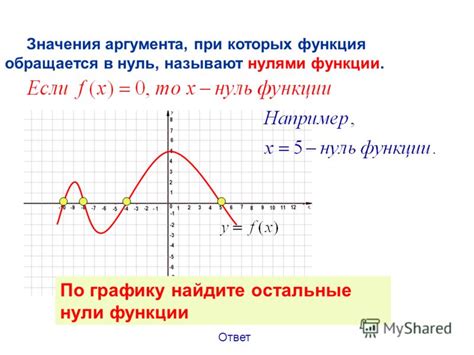
Нули функции являются важным понятием в математике и имеют широкое применение в различных областях. Они позволяют находить решения уравнений и уточнять значения функции в различных точках.
Например, рассмотрим функцию f(x) = x^3 - 2x^2 - 4x + 8. Чтобы найти нули этой функции, необходимо решить уравнение x^3 - 2x^2 - 4x + 8 = 0. Путем решения этого уравнения можно найти точки, в которых функция равна нулю.
Итак, нули функции f(x) = x^3 - 2x^2 - 4x + 8 являются решениями уравнения x^3 - 2x^2 - 4x + 8 = 0. Если решением является x = 2, то функция f(x) равна нулю при x = 2.
В общем случае, нули функции могут быть найдены различными методами, такими как графический метод, аналитический метод или численные методы. Знание нулей функции позволяет анализировать ее поведение, строить ее график и решать уравнения, связанные с данной функцией.
Понятие искомого значения
Понятием искомого значения называется значение переменной или функции, которое нужно найти в заданной ситуации или уравнении. В контексте функции, искомое значение часто называется значением функции в точке или аргументе, равном нулю.
Значение функции в точке или аргументе, равном нулю, называется нулём функции. Это значит, что при подстановке нуля в качестве аргумента функции, значение функции становится равным нулю.
Искомые значения нулями функции являются важными для нахождения различных характеристик функции, таких как экстремумы, точки перегиба, неравенства и т.д. Они также используются для решения уравнений, так как в уравнении часто нужно найти такие значения, при которых функция обращается в ноль.
Примеры искомого значения нулями функции могут включать нахождение корней уравнения или нахождение значений функции в конкретных точках. Например, при решении уравнения x^2 - 4 = 0, нужно найти такое значение x, при котором функция x^2 - 4 обращается в ноль. В данном случае, искомые значения будут x = -2 и x = 2.
Примеры функций с нулевыми значениями
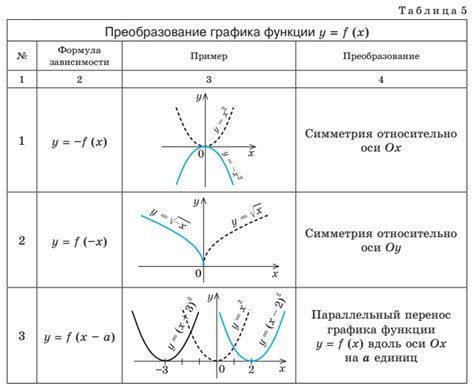
Вот некоторые примеры функций с нулевыми значениями:
- Линейная функция: f(x) = 0. Это пример прямой, которая проходит через начало координат и имеет нулевой угловой коэффициент. Все значения функции f(x) в этом случае равны нулю.
- Квадратичная функция: f(x) = x^2 - x. В этом случае значение функции равно нулю при x = 0 и x = 1.
- Тригонометрическая функция: f(x) = sin(x). У этой функции синуса значения равны нулю в точках x = 0, x = π и x = 2π.
- Экспоненциальная функция: f(x) = e^x - 1. Значение функции равно нулю при x = 0.
- Логарифмическая функция: f(x) = log(x). Значение функции равно нулю при x = 1.
Это лишь несколько примеров из множества функций с нулевыми значениями. Понимание и исследование нулевых значений функций помогает в решении уравнений и анализе кривых и поверхностей, что является важным инструментом в различных дисциплинах.
Значение нулями графика функции
Значение нулями графика функции может быть полезным для решения различных задач и исследования свойств функции. Оно позволяет определить корни функции, то есть значения аргумента, при которых функция равна нулю. Корни функции могут иметь различные значения и применения в различных областях науки и техники.
Примером функции, у которой значение нулями графика является особенно важным, является квадратное уравнение. Значение нулями графика квадратного уравнения позволяет найти его корни, которые могут использоваться для решения различных задач в математике и физике.
Значение нулями графика функции является важным инструментом для изучения и анализа функций. Оно позволяет определить точки, в которых функция равна нулю, и использовать эти значения для решения различных задач и построения графиков функций.
Нулевые точки и контекст задачи

Понимание нулевых точек функции позволяет нам находить решения уравнений, определять интервалы, на которых функция положительна, отрицательна или равна нулю, а также анализировать график функции.
В контексте задачи нулевые точки функции могут иметь различную интерпретацию. Например, если функция описывает положение тела в пространстве в зависимости от времени, то её нулевые точки могут соответствовать моментам времени, когда положение тела равно нулю. В случае, если функция описывает объем растущего или убывающего предприятия, нулевые точки будут означать моменты времени, когда объем равен нулю или происходит смена направления роста.
Примером может служить функция f(x) = x^2 - 4. Найдя нулевые точки этой функции, мы можем сказать, что они равны -2 и 2. В контексте задачи, например, нахождения корней квадратного уравнения x^2 - 4 = 0, эти нулевые точки будут означать значения аргумента, при которых уравнение имеет решение.
Свойства функций с нулевыми значениями
Функция с нулевым значением возвращает ноль при подстановке значений в ее аргументы. Такие функции могут иметь различные свойства, которые полезно знать, чтобы лучше понять их поведение и использование.
Вот некоторые из основных свойств функций с нулевыми значениями:
- Точка пересечения с осью абсцисс: нулевая функция имеет точку пересечения с осью абсцисс, так как значение функции равно нулю при значениях аргументов равных нулю.
- Симметрия относительно оси ординат: нулевая функция симметрична относительно оси ординат, так как значения функции симметричны относительно нулевого значения.
- Определение положительных и отрицательных значений: функция с нулевым значением может иметь положительные и отрицательные значения в зависимости от значения ее аргумента. Если аргумент функции положителен, то значение функции будет отрицательным, а если аргумент отрицателен, то значение функции будет положительным.
- Связь с другими функциями: нулевая функция может быть как независимой функцией, так и быть частью более сложной функции. Она может использоваться, например, для создания базовой линии в графиках или для определения показателей относительного изменения других функций.
Использование функций с нулевыми значениями зависит от конкретной задачи и контекста, но знание и понимание их свойств позволяет более эффективно использовать и анализировать такие функции.
Значение нулями функции и ее анализ
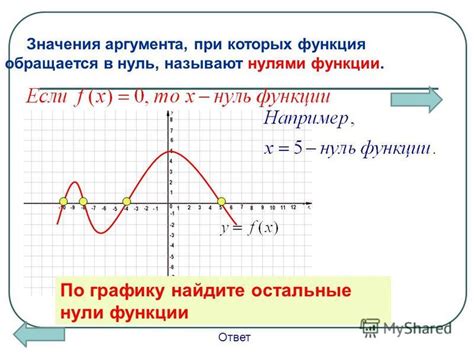
Для анализа нулей функции можно использовать график функции или алгоритмы решения уравнений. Если значение функции равно нулю в точке, то эта точка является нулем функции.
Анализ нулей функции позволяет определить следующие свойства:
- Количество нулей функции на заданном интервале;
- Интервалы возрастания и убывания функции;
- Экстремумы функции (максимумы и минимумы);
- Точки перегиба функции;
- Границы области определения функции;
- Другие особые точки и значения функции.
Нули функции могут помочь в поиске решений уравнений и систем уравнений, определении корней и факторизации функций.
Важно отметить, что нули функции могут быть дискретными или непрерывными в зависимости от типа функции и ее графика. Для непрерывных функций, в особенности, нули могут быть определены на отрезках или внутри интервалов.
Изучение нулей функции позволяет лучше понять ее поведение и решать задачи из различных областей математики и науки, где функции являются ключевыми понятиями.








