Уравнения являются основой алгебры и математики в целом. Однако, при решении уравнений, иногда возникают так называемые комплексные корни. Что это значит и как их находить?
Комплексные корни – это решения уравнений, которые находятся за пределами множества вещественных чисел. Они включают в себя воображаемую единицу i, которая определяется как квадратный корень из -1. Таким образом, комплексные числа представляют собой комбинацию вещественной и мнимой частей.
Для нахождения комплексных корней уравнений, необходимо использовать методы комплексного анализа и алгебры. Один из таких методов – метод подстановки комплексного числа в уравнение и приравнивания ему нулю. Затем происходит выделение вещественной и мнимой частей, что позволяет найти значения комплексных переменных, удовлетворяющих уравнению.
Примером уравнения с комплексными корнями может служить квадратное уравнение вида ax² + bx + c = 0. Если дискриминант этого уравнения отрицателен, то корни будут комплексными числами. Имея формулу дискриминанта и метод решения квадратных уравнений, можно вычислить комплексные корни данного уравнения.
Комплексные корни находят свое применение в различных областях математики, физики и инженерии. Они позволяют решать задачи, связанные с колебаниями, электрическими цепями, теорией вероятности и другими.
Что такое комплексные корни уравнения?
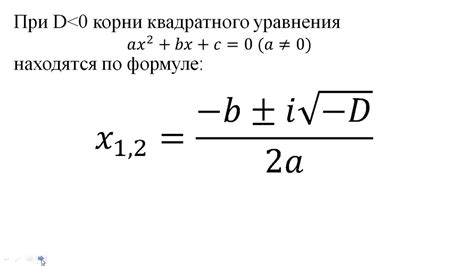
Когда решаем уравнение, в котором есть комплексные корни, мы получаем значения, которые нельзя представить в виде обычных действительных чисел. Вместо этого, комплексные корни уравнения представляют собой пары чисел, где одно число – это вещественная часть, а другое – мнимая.
Примеры комплексных корней могут быть следующими: 3 + 4i, 0 - 2i, 1.5 - 0.7i и так далее. Важно отметить, что комплексные корни всегда сопряжены, то есть если у нас есть корень a + bi, то его сопряженный корень будет иметь вид a - bi.
Комплексные корни встречаются, например, при решении квадратных уравнений, где дискриминант отрицателен. В таких случаях, решение уравнения включает в себя комплексные числа и называется комплексным решением.
Найти комплексные корни уравнения можно, используя различные методы, например, метод Формулы Кардано-Виета или радикалы.
Использование комплексных корней уравнения имеет важное практическое применение в различных областях науки и техники, таких как теория сигналов, электротехника, квантовая физика и другие.
Определение и представление
Комплексные корни уравнения можно представить в алгебраической форме и тригонометрической форме. Алгебраическая форма представления комплексного числа имеет вид a + bi, где a и b – действительные числа. Тригонометрическая форма представления комплексного числа имеет вид r(cosθ + isinθ), где r – модуль комплексного числа и θ – аргумент комплексного числа.
Для нахождения комплексных корней уравнения можно использовать методы алгебры и тригонометрии. Алгебраический метод основан на использовании формулы корней уравнения и замене в ней значений.
Тригонометрический метод основан на использовании формулы Эйлера, которая связывает тригонометрическое представление комплексных чисел с их алгебраическим представлением. Зная алгебраическую форму комплексного числа, можно легко получить его тригонометрическое представление и наоборот.
Алгебраические и тригонометрические формы

Комплексные числа могут быть представлены в двух формах: алгебраической и тригонометрической.
Алгебраическая форма представляет комплексное число в виде a + bi, где a и b - вещественные числа, а i - мнимая единица. В алгебраической форме вещественная часть a и мнимая часть b являются действительными числами.
Тригонометрическая форма представляет комплексное число в виде r(cos(θ) + isin(θ)), где r - модуль числа, а θ - аргумент числа. В тригонометрической форме модуль r и аргумент θ являются величинами, характеризующими комплексное число.
Для перевода числа из одной формы в другую используются соотношения:
Алгебраическая форма: a + bi => Тригонометрическая форма: r(cos(θ) + isin(θ))
r = √(a^2 + b^2)
θ = arctan(b/a)
Тригонометрическая форма: r(cos(θ) + isin(θ)) => Алгебраическая форма: a + bi
a = r*cos(θ)
b = r*sin(θ)
Переход от алгебраической формы к тригонометрической форме позволяет получить информацию о модуле и аргументе числа, что может быть полезно при решении уравнений с комплексными корнями.
Как находить комплексные корни уравнения?
Один из таких методов – метод Кардано. Он применяется для решения кубических уравнений. Для нахождения комплексного корня уравнения с помощью метода Кардано необходимо знать его коэффициенты и применить соответствующие формулы.
Другой метод – метод Феррари. Он применяется для решения уравнений четвертой степени. Для нахождения комплексных корней уравнения с помощью метода Феррари необходимо знать его коэффициенты и также применить соответствующие формулы.
Также можно использовать графический метод. Для этого необходимо построить график функции, заданной уравнением, и определить точки пересечения этой функции с осью абсцисс. Комплексные корни уравнения будут представлять собой точки на комплексной плоскости.
Известным методом для нахождения комплексных корней является метод Виета. Он позволяет сразу найти все корни уравнения, в том числе и комплексные. Для применения метода Виета необходимо знать сумму и произведение корней уравнения.
В качестве альтернативы можно использовать численные методы, такие как метод Ньютона или метод бисекции. Они позволяют численно находить корни уравнения в любом случае, включая случай комплексных корней.
| Метод | Описание |
|---|---|
| Метод Кардано | Применяется для решения кубических уравнений |
| Метод Феррари | Применяется для решения уравнений четвертой степени |
| Графический метод | Построение графика функции и определение точек пересечения с осью абсцисс |
| Метод Виета | Позволяет сразу найти все корни уравнения, включая комплексные |
| Численные методы | Метод Ньютона, метод бисекции и другие численные методы |
Метод подстановки

Для применения метода подстановки необходимо сначала найти вещественные корни квадратного уравнения, например через формулу дискриминанта. Затем найденные корни подставляются в исходное уравнение, заменяя поочередно комплексный корень на сумму вещественных корней.
Если в результате подстановки получается верное тождество, то найденная сумма вещественных корней является комплексным корнем исходного уравнения. В противном случае, нужно искать другие способы решения уравнения.








