В математике интеграл по поверхности является одним из основных понятий, используемых в анализе и геометрии. Он позволяет вычислить значение некоторой функции на поверхности и имеет множество практических применений.
Интеграл по поверхности определяется как предел интегральных сумм для функции, заданной на поверхности. Он вычисляется с помощью интегрирования функции по всем точкам поверхности с учетом ее площади и направления. Интеграл по поверхности может быть положительным, отрицательным или равным нулю в зависимости от значения функции на поверхности.
Применение интеграла по поверхности находится во многих областях науки и техники. Например, в физике интеграл по поверхности используется для вычисления потоков векторных полей, электрического и магнитного поля. В геометрии он позволяет вычислить площади поверхностей различных фигур. Интеграл по поверхности также применяется в компьютерной графике для создания реалистичных трехмерных моделей.
Взятие интеграла по поверхности является сложной и важной операцией в математике, которая позволяет решить множество задач в различных областях науки и техники. Понимание этого понятия и умение правильно его применять является неотъемлемой частью математической подготовки.
В заключение, интеграл по поверхности является мощным инструментом, который позволяет вычислять значение функции на поверхности. Он имеет широкое применение в различных научных и технических областях и требует хорошего понимания и умения его применять для решения задач.
Взятие интеграла по поверхности: основные принципы и методы

Для вычисления интеграла по поверхности применяют различные методы. Одним из основных методов является параметризация поверхности, которая позволяет записать координаты точек поверхности в виде функции двух параметров. После параметризации поверхности, интеграл по поверхности сводится к интегралу от функции двух переменных на плоскости.
Еще одним методом взятия интеграла по поверхности является использование векторного поля, касательного к поверхности. В этом случае, интеграл по поверхности представляется в виде интеграла от скалярного произведения векторного поля и нормали к поверхности.
Для вычисления интеграла по поверхности также применяются методы параметризации криволинейных поверхностей, оболочки поверхности, сведение к поверхностному или криволинейному интегралу и другие методы.
Интеграл по поверхности является важным инструментом в математике и физике, который находит широкое применение в различных областях науки и техники. Он позволяет решать сложные задачи, связанные с потоками, массами и энергией, которые распределены по поверхностям различной формы и сложности.
Что такое интеграл по поверхности?
Идея интеграла по поверхности заключается в разбиении поверхности на бесконечное количество бесконечно малых элементов поверхности, называемых площадными элементами. Затем производится суммирование значений функции на каждом из этих площадных элементов с учетом их площадей. Результатом является интеграл по всей поверхности, который представляет собой сумму всех значений функции на поверхности.
Применение интеграла по поверхности широко используется в различных областях науки и техники. Например, в физике он применяется для расчета потоков векторных полей, таких как электрические поля или магнитные поля. В геометрии он позволяет вычислять площадь поверхностей с заданной формой. В теплообмене он используется для расчета теплоотдачи от поверхностей. Визуализация медицинских данных также может быть основана на интеграле по поверхности.
Физический смысл и применение интеграла по поверхности

В физике интеграл по поверхности используется для расчета потока векторного поля через данную поверхность. Поток векторного поля представляет собой количество векторов, перпендикулярных поверхности, проходящих через нее за единицу времени. Интеграл по поверхности позволяет рассчитать сумму этих векторов и определить общий поток векторного поля через всю поверхность. Это позволяет ученным и инженерам изучать и анализировать различные физические явления, связанные с потоком вещества или заряда через поверхность.
Применение интеграла по поверхности также находится в аэродинамике и гидродинамике, где он используется для расчета давления или силы, создаваемой на тело движущейся или находящейся в жидкости или газе поверхности. Интеграл позволяет ученым и инженерам определить, как это давление или сила воздействуют на тело и прогнозировать его движение и поведение в таких условиях.
Кроме того, интеграл по поверхности позволяет решать задачи, связанные с геометрией и геодезией, например, расчет объема тела, ограниченного заданной поверхностью, или вычисление площади поверхности самой поверхности. Это широко применяемый инструмент, который помогает в анализе и изучении различных геометрических объектов и поверхностей.
Таким образом, интеграл по поверхности является важным математическим инструментом, который находит применение во многих областях науки и техники. Он позволяет рассчитывать физические величины, связанные с поверхностями, и изучать их свойства. Благодаря интегралу по поверхности мы можем получить больше информации о поверхности и использовать эту информацию для принятия важных решений в различных областях науки и техники.
Связь интеграла по поверхности с другими математическими объектами
Один из главных объектов, с которыми связан интеграл по поверхности, - это векторное поле. Интеграл по поверхности векторного поля позволяет вычислить поток этого поля через данную поверхность, что имеет важные практические применения, например, в физике и инженерии.
Понятие интеграла по поверхности также тесно связано с градиентом и дивергенцией векторного поля. Градиент позволяет вычислить вектор, указывающий направление наибольшего роста функции на поверхности, а дивергенция - измерить ее распределение в пространстве.
Интеграл по поверхности также может быть использован для вычисления массы или центра масс объекта, заданного поверхностью. Это особенно полезно в физике и механике, где такие вычисления позволяют предсказывать поведение системы и решать практические задачи.
Кроме того, интеграл по поверхности может быть использован для решения задач нахождения площади поверхности или вычисления потенциала электрического поля.
Таким образом, интеграл по поверхности играет важную роль в различных областях математики и ее приложений, обеспечивая основу для вычислений и анализа множества разнообразных физических и геометрических явлений.
Методы вычисления интеграла по поверхности
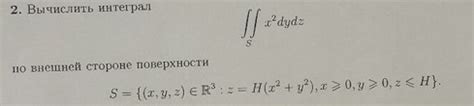
Вычисление интеграла по поверхности может быть выполнено различными методами. Некоторые из них представлены ниже:
- Метод параметризации поверхности: в данном методе поверхность параметризуется с помощью уравнений, что позволяет свести вычисление к интегралу по параметрам. Для этого выбираются параметры, по которым определяется положение точек на поверхности.
- Метод градиента: данный метод основан на использовании градиента поля, определенного на поверхности. Интеграл по поверхности сводится к интегралу от скалярного произведения градиента поля и вектора нормали к поверхности.
- Метод касательных плоскостей: в данном методе интеграл по поверхности аппроксимируется интегралом по касательной плоскости в точке поверхности и последующим интегрированием по всей поверхности.
- Метод поля токов: этот метод основан на представлении интеграла по поверхности в виде интеграла от скалярного произведения векторного поля и нормали к поверхности. Здесь используется понятие поля токов, которое характеризует поток векторного поля через поверхность.
Каждый из этих методов имеет свои особенности и может быть применен в зависимости от конкретной задачи. Выбор метода вычисления интеграла по поверхности зависит от сложности поверхности, свойств интегрируемой функции и требуемой точности результата.
Интеграл по поверхности в прямоугольной и полярной системах координат
В прямоугольной системе координат интеграл по поверхности вычисляется с помощью двойного интеграла:
- Выбирается параметризация поверхности в виде двух параметров u и v, описывающих координаты точек поверхности.
- Вычисляются производные координатных функций x(u,v), y(u,v) и z(u,v) по u и v.
- Интеграл по поверхности вычисляется как двойной интеграл от функции, заданной на поверхности, умноженной на дифференциалы площади элементов поверхности.
В полярной системе координат интеграл по поверхности вычисляется с помощью тройного интеграла:
- Выбираются параметризация поверхности в виде трех параметров r, φ и θ.
- Вычисляются производные координатных функций x(r, φ, θ), y(r, φ, θ) и z(r, φ, θ) по r, φ и θ.
- Интеграл по поверхности вычисляется как тройной интеграл от функции, заданной на поверхности, умноженной на дифференциалы площади элементов поверхности.
Интегралы по поверхности в прямоугольной и полярной системах координат широко используются в различных областях, таких как физика, геометрия и инженерия, для решения задач, связанных с распределением характеристик на поверхности. Понимание и правильное применение этих интегралов позволяет более точно описывать и анализировать поверхностные процессы и явления.
Вычисление интеграла по поверхности при помощи параметризации
Под параметризацией поверхности понимается замена переменных, при которой координаты точек поверхности выражаются через параметры. Таким образом, параметризация позволяет свести задачу вычисления интеграла по поверхности к задаче вычисления многомерного интеграла.
Параметризацию поверхности можно выбрать различными способами, в зависимости от характеристик поверхности и условий задачи. Например, для параметризации поверхности типа "параболоид" можно использовать параметры u и v, связанные с координатами x, y и z следующим образом:
| u | v | x(u,v) | y(u,v) | z(u,v) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | u | 0 | u^2 |
| 0 | 1 | 0 | v | v^2 |
Используя параметризацию, можно выразить искомый интеграл как интеграл от функции, зависящей от параметров u и v. Затем можно применить соответствующие методы вычисления многомерных интегралов, такие как метод Монте-Карло или метод прямоугольников.
Таким образом, параметризация поверхности позволяет существенно упростить вычисление интеграла по поверхности, представив его в более удобной форме. Этот метод находит широкое применение в физике, математике и других областях науки, где требуется вычислять объемы и площади фигур с нерегулярной формой.
Примеры решения задач с использованием интеграла по поверхности
Пример 1:
Пусть дана поверхность S, заданная уравнением x=rcos(θ), y=rsin(θ), z=f(x,y)=x^2+y^2, где r ≥ 0, 0 ≤ θ ≤ 2π. Найдем площадь поверхности S.
Решение:
Сначала найдем вектор нормали к поверхности S. Для этого нужно взять производные по параметрам r и θ, и нормализовать.
∂r/∂x=cos(θ), ∂r/∂y=sin(θ), ∂r/∂z=0
∂θ/∂x=-rsin(θ), ∂θ/∂y=rcos(θ), ∂θ/∂z=0
Тогда вектор нормали будет:
n = (∂r/∂x, ∂r/∂y, ∂r/∂z) × (∂θ/∂x, ∂θ/∂y, ∂θ/∂z) = (0, 0, r)
Для нахождения площади поверхности используется формула:
S = ∬S








