Несобственный интеграл — это понятие из математического анализа, которое определяет интеграл функции, не имеющей определенного значения на всем своем области определения. В отличие от собственного интеграла, несобственный интеграл вычисляется на бесконечных или бесконечно больших интервалах, либо в точках разрыва функции.
Вычисление несобственного интеграла — это задача нахождения приближенного результата такого интеграла. Для этого используются различные методы, включая метод замены переменной, интегрирование по частям, частные случаи несобственных интегралов и другие.
Один из примеров несобственного интеграла — интеграл от функции, у которой возникает бесконечность или разрыв на своей области определения. В таком случае, интеграл вычисляется как предел интеграла на ограниченной области, когда ее границы стремятся к бесконечности или точке разрыва.
Определение и основные понятия

Интеграл – это математическая операция, обратная процессу дифференцирования. Она позволяет находить площадь между функцией и осью абсцисс или найти функцию по ее первообразной.
Несобственный интеграл возникает в случае, когда функция не имеет определенного интеграла на заданном интервале из-за различных особенностей. Это может быть бесконечность функции в некоторых точках, разрывы, особенности в точках отрезка интегрирования или сходящийся интеграл в бесконечности.
Для вычисления несобственного интеграла необходимо проанализировать особенности функции и определить, какой именно тип несобственного интеграла представлен. Можно выделить два основных типа несобственных интегралов: интегралы первого и второго рода.
Интеграл первого рода зависит от особенностей функции на границах интервала интегрирования. В этом случае требуется подсчитать предел интеграла при приближении к границам интервала.
Интеграл второго рода оценивает особенности функции на всей области интегрирования. Здесь нужно анализировать поведение функции как внутри интервала, так и при приближении к его границам или бесконечности.
Вычисление несобственных интегралов может быть сложной задачей, требующей применения различных методов и приемов. Важно уметь анализировать особенности функций и выбирать подходящий подобласть интегрирования.
Понятие абсолютной и условной сходимости
Несобственные интегралы могут быть либо абсолютно сходящимися, либо условно сходящимися. Разница между ними заключается в сходимости интеграла только при условии сходимости модуля подынтегральной функции.
Абсолютно сходящийся интеграл определяется так: если модуль подынтегральной функции абсолютно интегрируем на заданном интервале интегрирования, то несобственный интеграл сходится абсолютно. То есть интеграл от модуля функции сходится.
Условно сходящийся интеграл определяется так: если интеграл функции сходится, но интеграл от модуля функции расходится, то несобственный интеграл сходится условно. В этом случае можно говорить о ряде Фурье для функции, которая задает функцию как сумму синусов и косинусов.
Для исследования сходимости несобственных интегралов вводится понятие интеграла Дирихле (обычный или вообще особый). Определение интеграла Дирихле имеет свои спецификации, которые необходимо учесть при анализе.
Таким образом, абсолютная и условная сходимость несобственных интегралов являются двумя различными вариантами сходимости интеграла.
| Абсолютная сходимость | Условная сходимость |
|---|---|
| Интеграл от модуля функции сходится | Интеграл от модуля функции расходится, но интеграл самой функции сходится |
Методы вычисления несобственных интегралов

Существует несколько методов для вычисления несобственных интегралов, которые используются в различных ситуациях. Рассмотрим некоторые из них:
Метод замены переменной – один из самых часто применяемых методов. Он заключается в замене переменной, чтобы свести задачу вычисления несобственного интеграла к задаче вычисления обычного интеграла. Подходящей заменой переменной можно упростить подынтегральную функцию и сделать ее интегрирование возможным.
Метод разложения на простые дроби – особый метод, используемый для вычисления несобственных интегралов с рациональной функцией в подынтегральном выражении. Он заключается в разложении рациональной функции на сумму простых дробей с неизвестными коэффициентами, которые затем можно найти приравниванием коэффициентов при соответствующих степенях переменной.
Метод интегрирования по частям – метод, основанный на формуле интегрирования по частям. Он используется при вычислении несобственных интегралов, когда подынтегральное выражение может быть представлено в виде произведения двух функций, одна из которых нужно проинтегрировать, а другая нужна для дифференцирования.
Метод предельного перехода – особый метод, который используется, когда несобственный интеграл содержит бесконечность в пределах интегрирования или в подынтегральном выражении. В этом случае несобственный интеграл вычисляется путем нахождения предела от обычного интеграла, когда один из пределов интегрирования стремится к бесконечности.
Метод дифференцирования под знаком интеграла – метод, который используется, когда необходимо проинтегрировать функцию, содержащую параметр, и затем производная этой функции необходима в выражении. Он заключается в дифференцировании несобственного интеграла по переменной в подынтегральном выражении и последующем интегрировании полученной функции.
Выбор метода для вычисления несобственного интеграла зависит от его характеристик и условий задачи. Часто требуется комбинированное применение нескольких методов для достижения результата.
Метод интегрирования по частям
Формула интегрирования по частям выглядит следующим образом:
∫ u dv = uv - ∫ v du
где u и v - функции, ∫ - интеграл, dv - дифференциал v и du - дифференциал u.
Для применения метода интегрирования по частям необходимо выбрать функции u и dv таким образом, чтобы производная функции u была легче вычисляема, чем сама функция u. Затем, используя формулу интегрирования по частям, можно преобразовать исходный интеграл и упростить его вычисление.
Применение метода интегрирования по частям может быть полезно, когда интегрируемая функция представляется в виде произведения двух функций, из которых одна сложнее вычисляется, чем другая.
При использовании метода интегрирования по частям необходимо учитывать, что иногда после применения формулы интегрирования по частям, получается новый несобственный интеграл, который также может потребовать применения этого метода повторно.
Применение метода интегрирования по частям требует навыков работы с дифференцированием и интегрированием, а также знания различных функций и формул для вычисления производных и интегралов. Поэтому для успешного применения данного метода рекомендуется ознакомиться с основными правилами дифференцирования и интегрирования.
Метод замены переменной
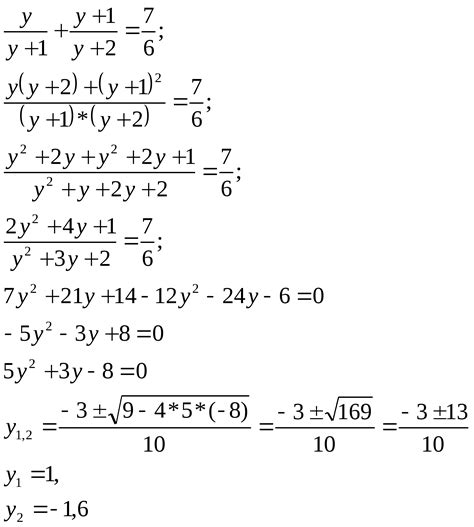
Для использования метода замены переменной необходимо:
- Выбрать подходящую замену переменной, которая позволит упростить интеграл.
- Выразить новую переменную через исходную и наоборот.
- Вычислить новые пределы интегрирования.
- Вычислить новый интеграл и вернуться к исходной переменной.
Применение метода замены переменной позволяет преобразовать сложный несобственный интеграл в более простую форму, что облегчает его вычисление. Основное условие успешного использования метода заключается в умении выбирать подходящую замену переменной, которая упростит интеграл и сделает его решение более доступным.
Использование метода замены переменной в сочетании с другими методами, например, интегрированием по частям, позволяет решать более сложные несобственные интегралы и получать точные результаты.
Метод дробно-линейной замены
Для применения метода дробно-линейной замены необходимо выполнить следующие шаги:
- Выполнить замену переменной: ax + b = t, где t – новая переменная.
- Выразить старую переменную через новую: x = (t - b) / a.
- Выразить дифференциал старой переменной через дифференциал новой переменной: dx = dt / a.
- Подставить полученные выражения в исходный несобственный интеграл и преобразовать его.
- Вычислить новый интеграл с помощью стандартных методов, таких как интегрирование по частям или метод замены переменной.
- Вернуться к исходной переменной и получить окончательный ответ.
Описанный метод позволяет существенно упростить вычисление несобственных интегралов, которые содержат дробно-линейную функцию. Применение этого метода требует некоторой тренировки и умения разбираться в алгебраических преобразованиях, но в итоге позволяет получать точные и наглядные ответы на поставленные интегральные задачи.
Практические примеры и решения

Для лучшего понимания, рассмотрим несколько примеров вычисления несобственных интегралов.
| Пример | Задача | Решение |
|---|---|---|
| Пример 1 | Вычислить несобственный интеграл ∫0∞ e-x dx | Пользуясь свойством несобственного интеграла, заменим верхний предел интегрирования на бесконечность: ∫0∞ e-x dx = lima→∞ ∫0a e-x dx Используем формулу интегрирования экспоненты: lima→∞ (-e-x)0a = lima→∞ (-e-a + 1) = 1 |
| Пример 2 | Вычислить несобственный интеграл ∫0∞ x2 dx | Применим формулу интегрирования степенной функции: ∫0∞ x2 dx = lima→∞ ∫0a x2 dx По формуле интегрирования степенной функции имеем: lima→∞ (x3/3)0a = lima→∞ (a3/3) = ∞ |
| Пример 3 | Вычислить несобственный интеграл ∫1∞ ln(x) dx | Заметим, что данная функция не определена при x ∫1a ln(x) dx Используя формулу интегрирования логарифма, получаем: ∫1a ln(x) dx = (x(ln(x) - 1))1a = a(ln(a) - 1) - (1(0 - 1)) = a(ln(a) - 1) + 1 Подставим верхний предел интегрирования a→∞: lima→∞ a(ln(a) - 1) + 1 = ∞ |
В данных примерах мы рассмотрели разные сценарии вычисления несобственных интегралов. В случае, когда интеграл сходится, можно получить точный результат, в противном случае, интеграл расходится и равен бесконечности.








