Внести под знак дифференциала – это понятие из математического анализа, которое используется для обозначения процесса перемещения некоторой величины в пределе. Внесение под знак дифференциала является одной из основных операций в дифференциальном исчислении и необходимо для вычисления интегралов по определенным функциям.
Для понимания этого понятия рассмотрим пример. Пусть имеется функция f(x), которая описывает зависимость какой-либо величины от переменной x. Для вычисления приращения этой величины на некотором интервале [a, b] можно воспользоваться интегралом от этой функции. Однако, чтобы интеграл был возможен, необходимо в этом случае внести под знак дифференциала функцию f(x) для последующего интегрирования.
Примером внесения под знак дифференциала может быть следующее уравнение:
Интеграл от функции f(x) = x^2 dx
В данном случае, для возможности интегрирования, нужно внести функцию x^2 под знак дифференциала dx. Это позволяет более удобным образом провести вычисления и получить точное значение интеграла.
Понятие и смысл дифференциала
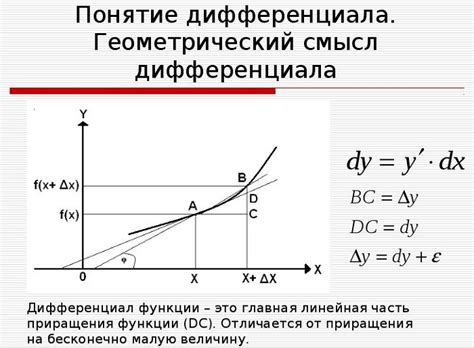
Внесение под знак дифференциала является операцией, которая используется для удобства при вычислении функций. Суть этой операции заключается в замене исходной функции на линейную функцию, являющуюся касательной к графику функции в заданной точке.
При внесении под знак дифференциала исходная функция заменяется на сумму трех слагаемых: дифференциал функции, произведение дифференциала независимой переменной и первой производной исходной функции по этой переменной, и остаточный член, который является бесконечно малой величиной высшего порядка.
Примером внесения под знак дифференциала может служить следующее:
Пусть у нас есть функция f(x) = x2. Чтобы вычислить дифференциал этой функции df, можно воспользоваться формулой:
df = f'(x) dx
где f'(x) - это производная функции f(x), а dx - дифференциал независимой переменной x.
Таким образом, внесение под знак дифференциала позволяет нам удобно вычислять изменение функции вблизи заданной точки и использовать это для различных математических операций и приложений.
Математическая формулировка внесения под знак дифференциала
Математическая формулировка внесения под знак дифференциала выглядит следующим образом:
Если: | f(x, y) - функция двух переменных; |
И: | dx и dy - дифференциалы переменных x и y соответственно; |
Тогда: | |
df(x, y) = (∂f/∂x)dx + (∂f/∂y)dy, | |
Где (∂f/∂x) и (∂f/∂y) – частные производные функции f(x, y) по переменным x и y соответственно.
Примером применения внесения под знак дифференциала может служить вычисление полного дифференциала функции.
Рассмотрим функцию z(x, y) = x^2 + y^2 - 2xy. Её полный дифференциал можно выразить с помощью введения дифференциалов переменных x и y:
dz = (∂z/∂x)dx + (∂z/∂y)dy |
= (2x - 2y)dx + (2y - 2x)dy |
Таким образом, зная частные производные функции z(x, y), мы можем выразить полный дифференциал этой функции с помощью внесения под знак дифференциала.
Примеры простейших функций
Ниже приведены некоторые примеры простейших функций, в которых вносятся под знак дифференциала:
- Функция 1: $$y = f(x)$$ - функция, представленная в виде одной переменной.
- Функция 2: $$y = f(x) + dx$$ - функция, в которой добавляется дифференциал переменной.
- Функция 3: $$y = f(x)dx$$ - функция, в которой дифференциал переменной умножается на функцию.
- Функция 4: $$y = f(x)g(x)dx$$ - функция, в которой дифференциал переменной умножается на произведение двух функций.
Примеры сложных функций
Внесение под знак дифференциала может быть применено к различным функциям, как простым, так и сложным. Некоторые примеры сложных функций включают в себя:
1. Косинус и синус:
d(sin x) = cos x dx
d(cos x) = -sin x dx
2. Экспонента и логарифм:
d(e^x) = e^x dx
d(ln x) = 1/x dx
3. Тригонометрические функции:
d(tan x) = sec^2 x dx
d(sec x) = sec x tan x dx
d(cosec x) = -cosec x cot x dx
d(cot x) = -cosec^2 x dx
4. Гиперболические функции:
d(sinh x) = cosh x dx
d(cosh x) = sinh x dx
d(tanh x) = sech^2 x dx
5. Показательная функция:
d(a^x) = ln a * a^x dx
Это лишь несколько примеров сложных функций, для которых можно применить внесение под знак дифференциала. В каждом конкретном случае необходимо учитывать правила дифференцирования и применять их соответственно.
Внесение под знак дифференциала в многомерных пространствах

Внесение под знак дифференциала основывается на теореме Фубини, которая утверждает, что если функция является абсолютно интегрируемой на прямоугольнике, то двойной интеграл может быть вычислен путем последовательного вычисления двух одномерных интегралов.
Процесс внесения под знак дифференциала можно представить на примере двойного интеграла. Пусть есть функция f(x, y), определенная на прямоугольнике [a, b] × [c, d]. Интеграл от f(x, y) по прямоугольнику можно записать как:
∫∫f(x, y) dxdy
Если область интегрирования можно представить как последовательную сумму прямоугольников, то можно внести дифференциалы под знак интеграла и записать интеграл как сумму двух одномерных интегралов:
∫∫f(x, y) dxdy = ∫ab∫cdf(x, y) dydx
Таким образом, внесение под знак дифференциала позволяет упростить вычисление интеграла по многомерной области интегрирования и изменить порядок дифференцирования и интегрирования.
Возможные ошибки при применении правила
При применении правила внесения под знак дифференциала могут возникать различные ошибки, которые необходимо учитывать и избегать. Некоторые из наиболее распространенных ошибок при работе с дифференциалами приведены ниже:
1. Неправильная запись функций: Важно правильно записывать функции в дифференциале, чтобы избежать ошибок. Например, если внести под знак дифференциала функцию вида f(x) + g(x), то правильно это записать как df(x) + dg(x), а не как d(f(x) + g(x)).
2. Некорректная замена переменных: При внесении под знак дифференциала часто используются замены переменных. Неправильная замена переменных может привести к ошибочным результатам. Важно быть внимательным при выборе и использовании замены переменных.
3. Неправильное применение правила: Правило внесения под знак дифференциала имеет свои ограничения и условия применения. Неправильное применение правила может привести к неверным результатам. Важно внимательно следовать правилам и учитывать условия применимости.
4. Неправильное определение дифференциала: Некорректное определение дифференциала может привести к ошибочным результатам. Важно правильно определить дифференциал и учесть его свойства и связи с исходной функцией.
5. Неправильная обработка констант: При работе с дифференциалами необходимо учитывать обработку констант. Некорректное учет констант может привести к ошибочным результатам. Важно правильно обрабатывать и учитывать константы при внесении под знак дифференциала.
Избегая данных ошибок и придерживаясь правил и условий применения, можно успешно вносить под знак дифференциала различные функции и получать корректные результаты.
Практическое применение правила в физике и экономике

Одним из примеров практического применения правила в физике является механика. Например, для определения работы силы, которая действует на тело, можно использовать правило внесения под знак дифференциала. Работа силы W может быть выражена как интеграл от скалярного произведения силы F и дифференциального перемещения ds по траектории движения тела:
W = ∫ F · ds
В экономике также можно применять правило внесения под знак дифференциала для анализа различных процессов. Например, для определения общего объема производства можно использовать интеграл от производного по времени объема производства:
Q = ∫ dQ/dt · dt
Это позволяет более точно оценить эффективность работы предприятия или определить технологический процесс производства.
Таким образом, правило внесения под знак дифференциала находит широкое применение в физике и экономике, позволяя более точно анализировать различные процессы и решать сложные задачи. Это является важным инструментом для развития научных и технических отраслей и принятия обоснованных решений.








