В логике, тождественная истинность формулы является основным понятием, которое описывает способность формулы быть истинной независимо от значений своих переменных. То есть, вне зависимости от того, какие значения принимают переменные в формуле, она всегда будет истинной.
Термин "тождественная истинность" часто используется в математической логике и представляет собой понятие абсолютной истины, безусловно верной во всех случаях. Такая формула не зависит от внешних условий или контекста, и ее истинность является незыблемой.
Одним из примеров тождественной истинности является формула "A или не А", где А - любая пропозициональная переменная. Вне зависимости от того, какое значение принимает переменная А, выражение всегда будет истинным. Например, если А принимает значение истины, то выражение становится истинным, так как "истина или не истина" является тавтологией. Если же А принимает значение лжи, то выражение также становится истинным, так как "ложь или не ложь" также является тавтологией.
Тождественная истинность формулы является важным концептом в логике, позволяющим определить абсолютную истину формулы независимо от значений ее переменных. Это понятие находит применение во многих областях, включая математику, философию и информатику.
Тождественная истинность формулы: что это такое?

Тождественная истинность формулы может быть полезной в различных областях, таких как математика, философия и информатика. Она позволяет устанавливать универсальные законы и принципы, которые верны в любых условиях.
Для понимания тождественной истинности формулы необходимо знать основные логические связки. Наиболее распространенные связки включают "и", "или", "не" и "если-то". Комбинируя эти связки, можно создавать формулы с разными утверждениями и определять их истинность.
Примером тождественно истинной формулы является закон исключенного третьего в логике: "или p, или не p". Независимо от значения переменной p, эта формула всегда будет истинной.
Тождественная истинность формулы является важным понятием в математической логике и помогает устанавливать общие законы и принципы, применимые в различных областях знаний. Понимание этого понятия позволяет проводить анализ и доказательства, основываясь на логических основах.
Определение и объяснение понятия
В логике утверждения могут быть выражены с помощью формул, составленных из логических операторов и переменных. Когда формула всегда истинна, она считается тождественно истинной. Другими словами, независимо от того, какие значения принимают переменные, формула всегда будет истинной.
Примером тождественно истинной формулы является формула "p ∨ ¬p", где "p" - переменная. В этой формуле используется оператор "ИЛИ" и оператор отрицания. Независимо от значения переменной "p", формула всегда будет истинной, так как она утверждает, что "p" истинно или истинно то, что отрицает "p".
Тождественная истинность формулы важна в контексте математики и компьютерных наук, где используется логическое рассуждение и проверка утверждений. При наличии тождественно истинной формулы можно быть уверенным в ее истинности независимо от значений переменных, что помогает в доказательствах и решении задач.
| Формула | Тождественная истинность |
|---|---|
| p ∨ ¬p | Да |
| p ∧ ¬p | Нет |
| ¬(p ∧ q) ↔ (¬p ∨ ¬q) | Да |
Зависимость тождественной истинности от логических операций
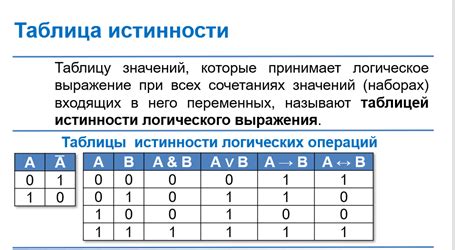
Тождественная истинность формулы зависит от применяемых в ней логических операций. Логические операции могут быть истинными или ложными в зависимости от значений своих входных аргументов. В случае, когда все входные аргументы операции истинны, операция называется тождественно истинной.
Примером такой операции является конъюнкция (логическое "И"). Формула, содержащая только конъюнкции, будет всегда истинной, если все входные аргументы истинны. Например, формула (p ∧ q) ∧ r будет тождественно истинной только в том случае, когда p, q и r истинны.
С другой стороны, операция дизъюнкции (логическое "ИЛИ") может быть тождественно истинной, если хотя бы один из входных аргументов является истинным. Например, формула (p ∨ q) ∨ r будет тождественно истинной, если хотя бы один из аргументов p, q или r истинен.
Важно отметить, что не все операции в логике могут быть тождественно истинными, например, операция отрицания (логическое "НЕ") не может быть тождественно истинной, так как она меняет истинность своего аргумента.
Доказательство тождественной истинности формулы
Метод математической индукции предполагает доказательство утверждения для базового случая, после чего установление индукционного перехода для общего случая. Если базовый случай и переход выполняются, можно заключить, что утверждение справедливо для всех возможных значений.
Логический вывод основан на применении правил логического следования для вывода истинности формулы из уже установленных истинных утверждений и правил логики. Каждый шаг вывода должен быть основан на правиле вывода, что позволяет получить истинность исходной формулы.
Примером доказательства тождественной истинности формулы может служить доказательство тождества Де Моргана:
Начальный шаг:
Пусть A и B – произвольные высказывания. Докажем, что ¬(A∨B) ≡ (¬A∧¬B).
Базовый случай:
Рассмотрим значения высказываний A и B. Если A = Ложь и B = Ложь, то:
¬(Ложь∨Ложь) ≡ ¬Ложь ≡ Истина
(¬Ложь∧¬Ложь) ≡ Истина∧Истина ≡ Истина
Индукционный переход:
Предположим, что формула ¬(A∨B) ≡ (¬A∧¬B) верна для произвольных значений A и B. Докажем, что она также верна для значений A = Истина и B = Ложь:
¬(Истина∨Ложь) ≡ ¬Истина ≡ Ложь
(¬Истина∧¬Ложь) ≡ Ложь∧Истина ≡ Ложь
Таким образом, по методу математической индукции доказано тождество Де Моргана: ¬(A∨B) ≡ (¬A∧¬B) для всех возможных значений A и B.
Примеры тождественно истинных формул

Тождественная истинность формулы означает, что данная формула верна для любых значений своих переменных. В математической логике и логике высказываний существует несколько формул, которые всегда истинны, независимо от значений переменных. Вот несколько примеров таких формул:
- Строки равны сами себе: В формальной логике можно сформулировать закон, который утверждает, что любая строка (формула) равна самой себе. Например, формула "A → (B ↔ A)" всегда истинна, независимо от значений переменных A и B.
- Противоречие: Существует формула, которая всегда ложна и не зависит от значений переменных. Например, формула "A ∧ ¬A" всегда является ложной.
- Тождество исключенного третьего: Закон исключенного третьего утверждает, что для любого высказывания A верно A ∨ ¬A. Это означает, что любое высказывание либо истинно, либо ложно.
Это лишь некоторые примеры тождественно истинных формул. Всего в математической логике существует множество таких формул, которые всегда верны и играют важную роль в выводах и доказательствах.
Роль тождественно истинных формул в математике и логике
Тождественно истинная формула - это высказывание, которое истинно независимо от значений переменных, которыми она заменена. Такая формула всегда истинна, независимо от контекста, в котором рассматривается.
В математике и логике тождественно истинные формулы используются, например, для определения логических законов и аксиом, которые являются основными принципами системы. Они помогают обосновывать логические выводы и следствия в рамках данной системы.
Примером тождественно истинной формулы может служить "Закон исключённого третьего", который гласит: "Для любого высказывания А, высказывание "А или не А" истинно". Эта формула всегда истинна, независимо от значения высказывания А.
Также тождественно истинные формулы используются при доказательстве теорем и теорий. Они могут быть использованы в качестве основы для применения различных методов и логических рассуждений.
Вывод: тождественно истинные формулы играют важную роль в математике и логике, являясь основой для доказательства других утверждений и формирования новых теорий. Они помогают обосновывать логические выводы и являются основными принципами системы.








