Прологарифмирование уравнения является одним из основных инструментов математического анализа и науки в целом. Этот метод позволяет упростить сложные математические выражения, а также найти решения сложных уравнений.
Прологарифмирование уравнения основано на применении логарифмической функции к обеим сторонам уравнения. Логарифм – это обратная функция к экспоненте и позволяет выразить аргумент, при котором получается данный результат.
Один из основных примеров использования прологарифмирования – решение экспоненциальных уравнений. Такие уравнения имеют вид a^x = b, где a и b – это известные числа, а x – искомая величина. Применяя прологарифмирование, можно найти значение x, исходя из заданных значений a и b.
Прологарифмирование уравнения является мощным инструментом в математике, физике, экономике и других науках. Оно позволяет упростить сложные выражения и найди решения сложных уравнений. Решая задачи, связанные с экспоненциальными функциями, невозможно обойтись без применения прологарифмирования. Знание основ данного метода позволяет более глубоко понять и анализировать математические и физические явления.
Для чего нужно прологарифмировать уравнение
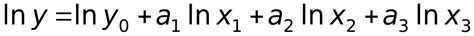
Прологарифмирование позволяет привести уравнение к более простой форме, где переменная степени скрывается под логарифмом. Это облегчает решение уравнения, так как позволяет использовать свойства логарифмов и алгебраических тождеств для упрощения выражений и нахождения значений переменных.
Кроме того, прологарифмирование широко применяется в различных научных и инженерных областях, где уравнения, содержащие экспоненты и показательные функции, встречаются часто. Например, в физике, химии и экономике применяются уравнения, описывающие рост, распад и изменение некоторых величин с течением времени.
Прологарифмирование также используется для проведения статистических анализов и решения задач оптимизации. Применение логарифмирования может помочь линеаризовать данные, сгладить экспоненциальное или нелинейное поведение и сделать модели и уравнения более поддающимися анализу и интерпретации.
Важно отметить, что прологарифмирование уравнения не всегда является обязательным. В некоторых случаях, когда уравнение содержит простые выражения или не содержит показательных функций, можно обойтись без применения логарифмов. Однако, в большинстве случаев прологарифмирование уравнения является полезным методом для упрощения выражений и получения более точных решений.
Требования к прологарифмированию уравнения
Во-первых, уравнение должно быть положительным, так как оно будет использовано в рамках логарифмической функции. Также следует учесть, что аргумент логарифма должен отличаться от нуля, иначе решение будет невозможно.
Во-вторых, при прологарифмировании уравнения необходимо учитывать свойства логарифмов. В частности, должно быть известное основание логарифма для корректного преобразования уравнения. Основанием часто является число e (2,71828), натуральный логарифм, или число 10 для десятичного логарифма. Это позволяет преобразовать уравнение с помощью свойств логарифмов до простой формы, где от переменной остается только одна степень.
Наконец, требуется умение работать с логарифмическими тождествами и правилами преобразования уравнений. Это включает использование свойств логарифмов, таких как логарифм произведения, частного, возведения в степень и корня.
Соблюдение этих требований позволит успешно прологарифмировать уравнение и получить правильное решение. Необходимо помнить, что в процессе прологарифмирования могут появиться дополнительные решения или ограничения на переменные, которые также следует учесть при последующем анализе уравнения.
| Требования к прологарифмированию уравнения: |
|---|
| 1. Уравнение должно быть положительным. |
| 2. Аргумент логарифма не должен быть равен нулю. |
| 3. Известное основание логарифма для преобразования уравнения. |
| 4. Знание логарифмических тождеств и правил преобразования. |
Как правильно прологарифмировать уравнение

Для прологарифмирования уравнения важно выбрать правильный базис логарифма. Часто используемыми базисами являются натуральный логарифм (логарифм по основанию $e$) и десятичный логарифм (логарифм по основанию 10).
Процесс прологарифмирования уравнения сводится к применению соответствующего логарифма на обе стороны уравнения с последующим применением свойств логарифмов для упрощения выражений.
Пример прологарифмирования уравнения:
| Исходное уравнение | Прологарифмированное уравнение |
|---|---|
| $2^x = 16$ | $\log_2(2^x) = \log_2(16)$ |
| $x = \log_2(16)$ | |
| $x = 4$ |
Правильное прологарифмирование уравнения позволяет получить аналитическое выражение для переменной и, в итоге, решить уравнение. Однако необходимо помнить, что при прологарифмировании уравнения могут возникать новые решения, которые не являются решениями исходного уравнения. Поэтому необходимо проверять полученные результаты, подставляя их обратно в исходное уравнение и убеждаясь в их справедливости.
Применение прологарифмирования в решении уравнений
Прологарифмирование может быть полезно в случаях, когда уравнение содержит переменные в степени или логарифмы. Прологарифмирование позволяет преобразовать сложные уравнения в более простые формы, которые могут быть решены с использованием базовых свойств логарифмов.
Процесс прологарифмирования заключается в применении логарифма к обеим сторонам уравнения в соответствии с правилами алгебры. Например, если уравнение имеет вид a^x = b, где a и b - некоторые числа, то прологарифмирование может быть выполнено следующим образом:
логарифмируем обе стороны уравнения:
log(a^x) = log(b)
применяем свойство логарифма log(a^x) = x * log(a):
x * log(a) = log(b)
разделим обе стороны уравнения на log(a):
x = log(b) / log(a)
Таким образом, мы использовали прологарифмирование для получения значения переменной x в уравнении a^x = b.
Прологарифмирование также может быть применено к другим типам уравнений, содержащих логарифмы, чтобы упростить их решение. Однако, необходимо помнить о возможности появления дополнительных решений, а также о допустимых ограничениях на значения переменных при использовании этого метода.
Примеры использования прологарифмирования

Прологарифмирование часто используется в математике и науках, связанных с ней, для облегчения работы с уравнениями, функциями и выражениями. Вот несколько примеров, где применяется прологарифмирование:
1. Решение экспоненциальных уравнений:
Экспоненциальные уравнения, в которых переменная содержится в показателе степени, могут быть сложными для решения. Прологарифмирование позволяет преобразовать экспоненциальное уравнение в логарифмическое, где переменная содержится в аргументе логарифма. Это облегчает решение уравнения путем применения свойств логарифмов.
2. Упрощение сложных выражений:
Прологарифмирование может использоваться для упрощения сложных математических выражений. Путем прологарифмирования выражения можно заменить экспоненты на логарифмы и использовать свойства логарифмов для упрощения выражения.
3. Графический анализ:
Логарифмирование может помочь в графическом анализе данных. Путем прологарифмирования данных можно преобразовать нелинейные зависимости в линейные и упростить анализ и визуализацию данных.
4. Расчеты с процентами и ставками:
Прологарифмирование может быть использовано для решения задач, связанных с процентами и ставками. Путем применения логарифмов можно решить уравнение для поиска неизвестной процентной ставки или времени, связанного с процентами.
Все эти примеры демонстрируют полезность прологарифмирования в математике и науках. Они помогают упростить вычисления, решения уравнений и анализ данных. Поэтому понимание и использование прологарифмирования является важным навыком для студентов и исследователей в различных областях.








