Значение приставки arc перед sin, cos: подробный разбор

Математические функции sin и cos широко используются в различных задачах, связанных с тригонометрией. Однако, иногда возникает необходимость в поиске обратной функции - той, которая позволит определить угол, соответствующий заданному значению sin или cos. В этом случае можно использовать приставку arc перед sin и cos.

Приставка "arc" означает "арккосинус" и "арксинус". Функция arcsin(x), обозначенная также как sin^-1(x), возвращает угол, значение синуса которого равно x. Арккосинус, обозначаемый как arccos(x) или cos^-1(x), возвращает угол, значение косинуса которого равно x.

Важно понимать, что значение приставки arc может быть неоднозначным. Например, для функции arcsin(x) существует бесконечное количество значений угла, которые удовлетворяют условию sin(angle) = x. В большинстве программных языков и калькуляторов возвращается одно из возможных значений. Аналогично, функция arccos(x) также может иметь несколько значений.

Значение приставки arc перед sin, cos

Приставка "arc" (арк) перед функциями sin и cos обозначает обратные тригонометрические функции, которые позволяют найти угол, значение которого равно указанному в скобках.

Например, функция arcsin(x) возвращает угол, значение синуса которого равно x. Аналогично, функция arccos(x) возвращает угол, значение косинуса которого равно x.

Значение угла, возвращаемое данными функциями, измеряется в радианах и находится в диапазоне [-π/2, π/2] для arcsin(x) и [0, π] для arccos(x).

Обратные тригонометрические функции могут использоваться для нахождения значения угла в треугольнике по известным значениям его сторон, а также для решения уравнений, связанных с тригонометрическими функциями.

Приставка "arc" является сокращением от "арккосинус" и "арксинус", что указывает на обратный характер данных функций.

Арксинус и обратный синус

Арксинус - это тригонометрическая функция, которая позволяет найти угол x, для которого sin(x) равен данному значению. Например, если sin(x) = 0.5, то арксинус от 0.5 равен 30 градусам или π/6 радианам.

Обратный синус имеет тот же смысл, что и арксинус, но обозначается по-другому. Результат обратного синуса - это угол, для которого sin(x) равен заданному числу. Например, если sin(x) = 0.5, то sin^-1(0.5) равен 30 градусам или π/6 радианам.

С помощью арксинуса и обратного синуса можно решать различные задачи, связанные с треугольниками и углами. Они являются важными инструментами в математике и физике.

Для вычисления арксинуса и обратного синуса можно использовать таблицы значений или специальные калькуляторы. В языке программирования можно воспользоваться соответствующими функциями, такими как arcsin и asin.

sin(x)	Значение x
0	0
0.5	π/6
1	π/2

В таблице представлены некоторые значения sin(x) и соответствующие им значения x.

Использование арксинуса и обратного синуса требует осторожности, так как они имеют ограниченную область определения и область значений. Например, арксинус может быть определен только для значений от -1 до 1.

Арккосинус и обратный косинус

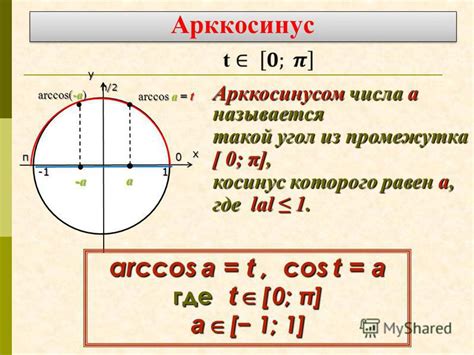
Арккосинус (arccos) обозначается как acos(x), где x - значение косинуса, а обратный косинус (cos⁻¹) обозначается как cos⁻¹(x). Оба этих терма возвращают угол (в радианах), значение косинуса которого равно x.

Арккосинус (арккос) и обратный косинус обладают следующими свойствами:

Они ограничены в диапазоне от 0 до π (0 ≤ arccos(x) ≤ π).
Если значение аргумента находится в диапазоне ±1 (-1 ≤ x ≤ 1), то оба терма возвращают угол в радианах.
Если значение аргумента находится вне диапазона (-∞
Обратный косинус является функцией, которая обратна к косинусу, то есть cos⁻¹(cos(x)) = x для всех значений x, где 0 ≤ x ≤ π.

Арккосинус и обратный косинус широко используются в различных областях науки, инженерии и математике. Они применяются, например, в вычислительной геометрии, физике и инженерных расчетах.

Арктангенс и обратный тангенс

Функция arctan(x) возвращает угол, для которого тангенс равен x. Например, arctan(1) возвращает значение π/4, так как тангенс(π/4) равен 1.

Обратная функция atan(x) возвращает такой угол, что его тангенс равен x. Например, atan(1) возвращает значение π/4, так как тангенс(π/4) равен 1.

Функции arctan(x) и atan(x) возвращают углы в радианах.

Арктангенс и обратный тангенс являются важными функциями в тригонометрии и математике в целом. Они используются в широком спектре задач, связанных с вычислительной и прикладной математикой, физикой, инженерией и другими науками.

Арккотангенс и обратный котангенс

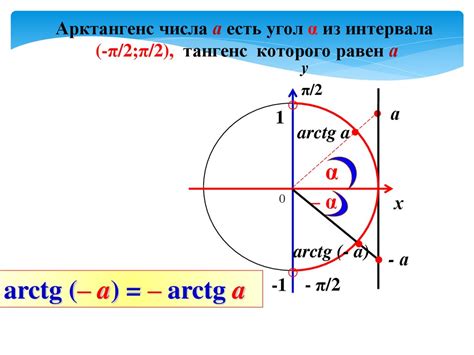
В математике приставка "arc" перед функциями sin, cos, tan, cot, sec, csc используется для обозначения обратных или арктангенс, арккосинус, арксинус, арккотангенс, арккотангенс, арксеканс и арккосеканс.

Арккотангенс - это обратная функция тангенса. Обозначается как arctan или atan. Арккотангенс угла a можно получить, вычислив значение тангенса этого угла и затем находя угол, тангенс которого равен полученному значению. Имеет область значений от -π/2 до π/2 радиан.

Обратный котангенс, или арккотангенс, - это обратная функция котангенса. Обозначается как arccot или acot. Обратный котангенс угла a можно получить, вычислив значение котангенса этого угла и затем находя угол, котангенс которого равен полученному значению. Имеет область значений от 0 до π радиан.

Арккотангенс и обратный котангенс часто используются в тригонометрии и математическом анализе для решения задач, связанных с вычислением углов и нахождением значений тангенса и котангенса.

Арксеканс и обратный секанс

Функция арксеканс возвращает значение угла, чей секанс равен x. То есть, если sec(θ) = x, то arcsec(x) = θ. При этом значение угла будет лежать в пределах (-π/2, π/2) и измеряться в радианах.

Функция обратного секанса asec(x) возвращает значение угла, чей косеканс равен x. То есть, если csc(θ) = x, то asec(x) = θ. При этом значение угла будет лежать в пределах (-π/2, π/2) и измеряться в радианах.

Использование арксеканса и обратного секанса может быть полезным в решении уравнений и задач, связанных с треугольниками и тригонометрическими функциями.

Арккосеканс и обратный косеканс

Арккосеканс определяется следующим образом:

arccsc(x) = арккосеканс x = угол, такой что csc угла равен x

Также можно записать:

arccsc(sin(x)) = x

где x - угол в радианах или градусах.

Причем значения арккосеканса лежат в интервале [-π/2, π/2] (в радианах) или [-90°, 90°] (в градусах).

Обратный косеканс (обозначается как csc^-1) - это обратная функция к косекансу. Он позволяет найти угол, значение косеканса которого равно заданному числу.

Обратный косеканс определяется следующим образом:

csc^-1(x) = обратный косеканс x = угол, такой что csc угла равен x

Также можно записать:

csc^-1(sin(x)) = x

где x - угол в радианах или градусах. Обратный косеканс также имеет значения в интервале [-π/2, π/2] (в радианах) или [-90°, 90°] (в градусах).

Свойства арктригонометрических функций

Арксинус (arcsin)

Функция арксинус сопоставляет каждому значению от -1 до 1 угол, который имеет этот синус. То есть, если указать значение sin(x), функция arcsin(x) вернет значение угла x в радианах, удовлетворяющего данному значению.

Свойства арксинуса:

1. Область значений: [-π/2, π/2]

2. Аргументы: от -1 до 1

3. Не является периодической функцией

4. График функции арксинуса является ограниченным сверху и снизу, симметричен относительно оси y=x и имеет точку перегиба в x=0.

Арккосинус (arccos)

Функция арккосинус определяет значение угла, косинус которого равен аргументу функции. То есть, если указать значение cos(x), функция arccos(x) вернет значение угла x в радианах, удовлетворяющего данному значению.

Свойства арккосинуса:

1. Область значений: [0, π]

2. Аргументы: от -1 до 1

3. Не является периодической функцией

4. График функции арккосинуса является ограниченным сверху и снизу, симметричен относительно оси y=x и имеет точку перегиба в x=0.

Формулы связи между арктригонометрическими функциями

Таким образом, приставка "arc" (от латинского "arcus", что означает "дуга") указывает на обратную функцию арктригонометрии. Например, функция arcsin(x) ищет такой угол, что его синус равен x.

Существует ряд формул связи между арктригонометрическими функциями, которые позволяют выразить одну арктригонометрическую функцию через другую. Некоторые из них:

1. Формула суммы:

где:

arcsin(x) + arccos(x) = π/2
arcsin(x) - arccos(x) = arcsin(x)
arcsin(x) = π/2 - arccos(x)

2. Формула произведения:

где:

arcsin(x) + arccos(x) = π/2
arcsin(x) - arccos(x) = arcsin(x)
arcsin(x) = π/2 - arccos(x)

3. Формулы двойного аргумента:

sin(2arcsin(x)) = 2x * sqrt(1 - x²)

cos(2arccos(x)) = 2x² - 1

Используя эти и другие формулы, можно связать различные арктригонометрические функции и решать задачи, связанные с нахождением углов или значений тригонометрических функций.

Особенности использования арктригонометрических функций

Одна из особенностей использования арктригонометрических функций состоит в их областях определения и значениях. Например, функция арксинус (asin) возвращает значение угла между -π/2 и π/2, то есть между -90° и 90°. Арккосинус (acos) возвращает значение угла между 0 и π, то есть между 0° и 180°.

Для использования арктригонометрических функций необходимо учесть их области определения, чтобы избежать ошибок и получить корректные результаты. Например, при вычислении арксинуса (asin) необходимо убедиться, что передаваемое значение находится в интервале [-1, 1], так как синус (sin) принимает значения только в этом диапазоне. В противном случае, возможна получения некорректного результата или ошибки.

Также стоит учитывать, что арктригонометрические функции возвращают значения в радианах, а не в градусах. Если требуется получить значение в градусах, необходимо выполнить соответствующее преобразование. Например, умножение на 180/π для перевода радиан в градусы.

Используя арктригонометрические функции, можно решать различные задачи, связанные с геометрией, физикой, инженерией и другими науками. Их применение позволяет находить углы, на основе известных значений тригонометрических функций, что является важной составляющей во многих областях науки и техники.

Примеры решений задач с использованием арктригонометрических функций

Для понимания применения арктригонометрических функций, рассмотрим несколько примеров с использованием функций arcsin и arccos.

Пример 1:

Найдем значение угла АВС, если известны значения сторон треугольника: AC = 6, BC = 8 и AB = 10.

Используем формулу для нахождения значения угла:

AB^2 = AC^2 + BC^2 - 2 * AC * BC * cos(∠BCA)
∠BCA = arccos((AC^2 + BC^2 - AB^2) / (2 * AC * BC))

Подставляя значения сторон треугольника, получим:

∠BCA = arccos((6^2 + 8^2 - 10^2) / (2 * 6 * 8)) = arccos(20 / 48) = arccos(5 / 12)

Ответ: угол АВС равен arccos(5 / 12) или около 65.06 градусов.

Пример 2:

Найдем значение угла АВС, если известны значения сторон треугольника: AC = 5, BC = 11 и AB = 13.