Первая производная функции является фундаментальным понятием в математическом анализе. Она позволяет определить скорость изменения значения функции в каждой точке ее области определения. В простых словах, первая производная показывает, насколько функция меняется при малых изменениях ее аргумента.
Определение первой производной функции включает ряд математических операций, таких как умножение, деление и предел. Первая производная может быть представлена в виде функции или числа, в зависимости от конкретной задачи.
Применение первой производной функции включает решение широкого спектра задач в различных областях науки и техники. Например, она позволяет определить экстремумы функции, т.е. ее наибольшие и наименьшие значения. Также первая производная используется для анализа графиков функций и определения особенностей их поведения.
Важно отметить, что первая производная несет важную информацию о функции, ее поведении и свойствах. Поэтому понимание значения первой производной функции является ключевым моментом для детального анализа и решения математических задач.
Определение первой производной

Математически первую производную функции можно определить с использованием предела:
f'(x) = limh→0 [(f(x + h) - f(x)) / h]
где f(x) – исходная функция, x – значение независимой переменной, а h – бесконечно малое приращение независимой переменной.
Первая производная может иметь различные значения в разных точках функции. Используя значения первой производной, можно анализировать график функции и описывать её поведение в различных областях определения, то есть определять интенсивность изменения функции (рост или убывание), точки экстремума, перегибы и другие характеристики.
На практике первая производная функции применяется во многих областях, таких как физика, экономика, биология и др. Она позволяет анализировать графики и моделировать процессы изменения величин и тенденции.
Геометрическая интерпретация первой производной
Первая производная функции имеет геометрическую интерпретацию, которая позволяет понять ее физический смысл и применение в реальной жизни. Она показывает, как меняется функция в зависимости от изменения ее аргумента.
Графически геометрическая интерпретация первой производной означает, что значение первой производной в точке определяет наклон касательной к графику функции в данной точке. Если значение первой производной положительно, то касательная будет иметь положительный угол наклона, указывающий на рост функции. Если значение первой производной отрицательно, то касательная будет иметь отрицательный угол наклона, указывающий на убывание функции. Если значение первой производной равно нулю, то касательная будет горизонтальной.
Таким образом, геометрическая интерпретация первой производной позволяет понять, как функция изменяется в данной точке и предоставляет информацию о тенденциях ее поведения. Это позволяет применять первую производную в различных областях, таких как физика, экономика, биология и многие другие.
Пример:
Предположим, у нас есть функция, описывающая скорость движения тела в зависимости от времени. Если мы возьмем первую производную этой функции в определенный момент времени, то сможем определить, увеличивается ли скорость тела или уменьшается. Если значение первой производной положительно, это будет означать ускорение тела. Если значение первой производной отрицательно, это будет означать замедление тела. Таким образом, первая производная функции в данном контексте имеет геометрическую интерпретацию, которая позволяет нам понять, как меняется скорость тела в зависимости от времени.
Точка экстремума: значение первой производной
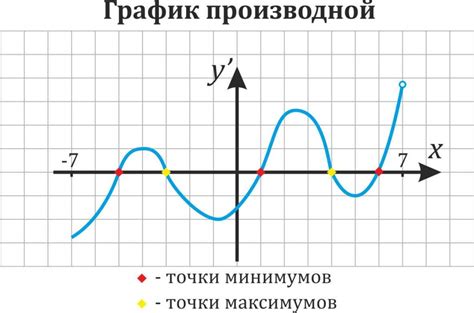
Для функции f(x), значение первой производной f'(x) в точке x=а позволяет сделать следующие выводы:
- Если f'(a) > 0, то функция возрастает в точке x=a. Это означает, что точка a является точкой локального минимума.
- Если f'(a)
- Если f'(a) = 0, то нельзя сделать однозначного вывода о характере точки a. Ее может объединять соседство точек минимума и максимума.
Значение первой производной функции в точке экстремума также помогает определить направление функции перед и после этой точки.
- Если f'(a) > 0, то функция возрастает перед точкой x=a и убывает после нее.
- Если f'(a)
Значение первой производной в точке экстремума играет важную роль в анализе функций и позволяет определить характер и направление функции вблизи этой точки.
Интервалы возрастания и убывания функции
Интервалы возрастания функции - это интервалы, на которых значение первой производной положительно. То есть, если производная положительна на интервале, то функция возрастает на этом интервале.
Аналогично, интервалы убывания функции - это интервалы, на которых значение первой производной отрицательно. Если значение производной отрицательно на интервале, то функция убывает на этом интервале.
Чтобы найти интервалы возрастания и убывания функции, необходимо решить уравнение производной равное нулю и применить тест знаков на полученных интервалах, а также рассмотреть значения производной в точках экстремумов.
Интервалы возрастания и убывания функции играют важную роль в анализе ее поведения и в определении экстремальных точек. Они также позволяют определить промежутки, на которых функция монотонна и строго монотонна.
Понимание интервалов возрастания и убывания функции позволяет лучше понять график функции и ее поведение на различных участках. Они являются важными инструментами для исследования функций, а также при решении задач из различных областей математики, физики, экономики и других наук.
Точки перегиба и вторая производная
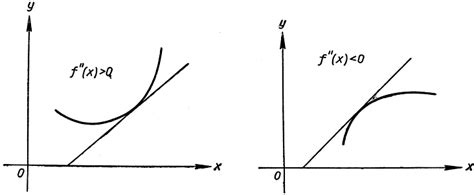
При изучении функций и их производных важно знать о существовании точек перегиба. Точки перегиба определяются как места на графике функции, где ее выпуклость меняется. В этих точках вторая производная функции равна нулю или не существует.
Вторая производная функции позволяет определить ее выпуклость и точки перегиба. Если вторая производная положительна на некотором интервале, то функция выпукла в этом интервале. Если вторая производная отрицательна, то функция вогнута. Точка перегиба определяется как точка, в которой выпуклость функции меняется.
Для нахождения точек перегиба требуется применить два шага. Вначале находят значения x, при которых вторая производная равна нулю или не существует. Затем, из этих значений выбирают те, которые находятся в интервалах, где выпуклость функции меняется. Такие точки будут точками перегиба.
Для проиллюстрации процесса определения точек перегиба, можно использовать таблицу. Ниже представлена таблица, в которой приведены значения x, значения второй производной f''(x), а также интервалы, в которых выпуклость функции меняется.
| x | f''(x) | Интервал выпуклости |
|---|---|---|
| x1 | 0 | В интервале (-∞, x1) и (x1, x2) |
| x2 | не существует | В интервале (x1, x2) и (x2, ∞) |
Таблица позволяет легко определить значения x, при которых функция изменяет выпуклость. Эти значения x в точности соответствуют точкам перегиба графика функции.








