Нормализация числа - это процесс приведения числа к определенному диапазону или пределам. Это может быть полезным при анализе данных или при работе с большими числами. Нормализация чисел позволяет сравнивать и обрабатывать их более эффективно.
Нормализация чисел часто используется в области машинного обучения и статистики. В машинном обучении, например, нормализация чисел может быть необходима для повышения точности модели, ускорения процесса обучения и предотвращения проблем с выбросами.
Чтобы нормализовать число, необходимо выполнить следующие шаги:
- Определить диапазон значений числа, к которому необходимо его привести.
- Вычислить минимальное и максимальное значения числа в исходном наборе данных.
- Применить формулу для нормализации числа, например, (x - min) / (max - min).
Например, у нас есть набор данных, содержащий числа от 100 до 1000. Если мы хотим нормализовать числа таким образом, чтобы они находились в диапазоне от 0 до 1, мы должны вычислить минимальное и максимальное значение (100 и 1000 соответственно) и применить формулу (x - 100) / (1000 - 100).
Что значит нормализуйте число?

Нормализация числа может понадобиться, например, когда сравниваются числа, представленные в разных системах счисления или записанные в разных форматах, таких как десятичный, двоичный или шестнадцатеричный. Также нормализация может быть полезной при работе с числами разных порядков и масштабов.
Одним из распространенных методов нормализации чисел является представление числа в научной нотации. Например, число 4500 в научной нотации будет выглядеть как 4.5 х 10^3. Это позволяет легко сравнить число с другими числами в научной нотации и более удобно выполнять математические операции.
Другой пример нормализации числа - представление числа в виде десятичной дроби. Например, число 0.0024 может быть представлено в виде десятичной дроби как 2.4 х 10^(-3). Это также позволяет более удобно сравнивать и выполнять операции с числами, записанными в десятичной дроби.
| Исходное число | Нормализованное число |
|---|---|
| 4500 | 4.5 х 10^3 |
| 0.0024 | 2.4 х 10^(-3) |
Понятие нормализации числа
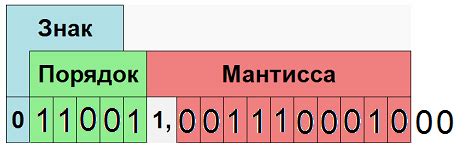
В основе нормализации лежит принцип представления чисел в виде числа с плавающей точкой, где значащая цифра находится перед десятичной точкой, а порядок величины - после. В этом виде все числа записываются с одинаковым числом значащих цифр и единственной десятичной цифрой.
Процесс нормализации числа включает несколько этапов:
- Перестановка запятой: Необходимо перенести плавающую точку так, чтобы получить целую часть числа, затем вычислить порядок величины перемещенной запятой.
- Округление и дополнение нулями: Если результат вычисления порядка величины получается отрицательным, необходимо оставить только целую часть числа и дополнить остальные разряды нулями. В противном случае, округлить число до заданной цифры после запятой.
- Добавление порядка величины: Нормализованное число записывается в виде значащей цифры, после которой идет буква E (от англ. exponent), затем сохраняется порядок величины.
Нормализация числа помогает представить его в виде, удобном для анализа, сравнения и совершения математических операций. Это широко применяется в научных и инженерных расчетах, а также в компьютерной графике и вычислениях.
Пример:
Исходное число: 345.678
Перестановка запятой: 3.45678
Результат округления и дополнения нулями: 3.456780000
Добавление порядка величины: 3.45678E0
Примеры нормализации чисел

1. Нормализация в диапазоне от 0 до 1:
Исходное число: 45
Минимальное значение: 0
Максимальное значение: 100
Нормализованное значение: 0.45
2. Нормализация с использованием стандартного отклонения:
Исходные числа: 10, 20, 30, 40, 50
Среднее значение: 30
Стандартное отклонение: 15
Нормализованные значения: -0.67, -0.33, 0, 0.33, 0.67
3. Нормализация с использованием единицы измерения:
Исходное число: 500 долларов
Минимальное значение: 0 долларов
Максимальное значение: 1000 долларов
Нормализованное значение: 0.5
Нормализация чисел позволяет сравнивать и анализировать различные наборы данных, упрощает вычисления и облегчает интерпретацию результатов. Она широко используется в областях, таких как машинное обучение, статистика и финансовая аналитика.
Причины нормализации чисел
1. Унификация представления Одна из основных причин нормализации чисел - это унификация представления чисел. Нормализованное число имеет одну и ту же форму представления для всех эквивалентных значений. Это позволяет упростить операции с числами, сравнивать их и выполнять другие математические операции. | 2. Предотвращение ошибок Нормализация чисел также помогает предотвратить ошибки, связанные с округлением и арифметическими операциями над числами. Когда числа нормализуются, вероятность возникновения ошибок уменьшается, так как вычисления производятся с использованием стандартных форм и правил. |
3. Уменьшение памяти и вычислительных ресурсов Нормализация чисел позволяет уменьшить объем памяти и вычислительных ресурсов, необходимых для хранения и обработки чисел. Нормализованные числа могут быть более компактными и требовать меньше операций для их обработки. | 4. Совместимость с другими системами В некоторых случаях нормализация чисел необходима для обеспечения совместимости с другими системами или форматами. Например, если число используется для передачи данных между различными системами, его нормализация может быть необходима для правильного интерпретирования числа во всех системах. |
Применение нормализации чисел
- В экономике и финансовой сфере нормализация чисел позволяет сравнивать и анализировать данные о доходах, расходах, инвестициях и прочих финансовых показателях разных компаний или стран.
- В научных исследованиях и статистике нормализация чисел помогает сравнивать данные, полученные из разных экспериментов или наблюдений, и выявлять паттерны, тренды и связи между ними.
- В машинном обучении и искусственном интеллекте нормализация чисел является важным шагом перед обучением модели на данных. Это позволяет улучшить сходимость алгоритмов обучения и повысить стабильность работы моделей.
В целом, нормализация чисел позволяет привести данные к одному и тому же масштабу и диапазону, что упрощает их анализ, сравнение и интерпретацию. Это важный инструмент для работы с числовыми данными в различных областях и помогает извлекать максимальную информацию из имеющихся данных.








