Тригонометрические уравнения являются одной из основных тем математики, их решение позволяет нам изучать свойства и взаимосвязи тригонометрических функций. Они находят применение в различных областях, включая физику, инженерию и естественные науки.
Основные простейшие тригонометрические уравнения имеют вид sin(x) = 0, cos(x) = 0 и tan(x) = 0. Их решение требует знания основных свойств тригонометрических функций и применения алгебраических методов.
Процесс решения простейших тригонометрических уравнений включает в себя выражение тригонометрических функций через их аргументы, применение свойств синуса, косинуса и тангенса, а также приведение уравнений к эквивалентным уравнениям.
Особенностью решения тригонометрических уравнений является периодичность тригонометрических функций. Для того чтобы найти все решения уравнения в заданном интервале, необходимо рассмотреть все значения аргумента, удовлетворяющие условию уравнения в этом интервале.
Тригонометрические уравнения: общая информация

В общем виде тригонометрическое уравнение может иметь следующий вид:
| функция | равенство | аргумент |
| sin, cos, tan, cot | равно | константа или выражение с переменными |
Основная цель решения тригонометрического уравнения - найти все значения переменных, при которых уравнение выполняется.
Чтобы решить тригонометрическое уравнение, можно использовать различные методы, в зависимости от его типа. Существуют общие методы, которые применимы к различным типам уравнений, а также специфические методы, разработанные для решения конкретных классов уравнений.
Общим методом решения тригонометрических уравнений является переход к эквивалентному уравнению без тригонометрических функций. Для этого используются тригонометрические тождества и формулы. Затем полученное уравнение решается с использованием алгебраических методов.
Некоторые известные классы тригонометрических уравнений: линейные, квадратные, кубические, биквадратные, трехчленные, двухчленные и другие. Каждый класс имеет свои особенности и специфические методы решения.
Знание тригонометрических уравнений позволяет решать множество задач из различных областей, таких как физика, геометрия, серия функцей и другие.
Что такое тригонометрическое уравнение?
Тригонометрические уравнения могут иметь разнообразные виды: линейные и квадратичные, одночленные и многочленные, а также уравнения смешанного типа. Они возникают при решении задач из различных областей: физики, геометрии, механики, астрономии и т.д.
Основным методом решения тригонометрических уравнений является приведение уравнения к эквивалентному уравнению, содержащему только одну тригонометрическую функцию. Для этого используются различные тригонометрические тождества и свойства функций.
Важно отметить, что тригонометрические уравнения могут иметь бесконечное множество решений или не иметь их вовсе. В таких случаях задача состоит в нахождении всех решений или определении условий, при которых уравнение имеет решения.
Решение тригонометрических уравнений требует хорошего знания тригонометрии и ее свойств, а также умения применять различные методы алгебры и анализа. Поэтому при изучении данной темы рекомендуется закреплять материал решением практических задач и использованием специальных таблиц и формул.
Простейшие тригонометрические уравнения: особенности и примеры

К особенностям простейших тригонометрических уравнений относится то, что они могут иметь бесконечное количество решений, в зависимости от значения переменной угла. Например, функция синус имеет период 2π, поэтому все значения функции повторяются с периодичностью 2π. Это означает, что уравнение sin(x) = 0 имеет бесконечное количество решений x = nπ, где n - любое целое число.
Одним из основных методов решения простейших тригонометрических уравнений является использование тригонометрических тождеств. Например, для решения уравнения sin(x) = 1/2 можно использовать тождество sin(π/6) = 1/2, что приводит к решению x = π/6 + 2πn, где n - любое целое число.
Приведем несколько примеров простейших тригонометрических уравнений:
| Уравнение | Решение |
|---|---|
| cos(x) = 0 | x = π/2 + πn, где n - любое целое число |
| tan(x) = 1 | x = π/4 + πn, где n - любое целое число |
| sin(2x) = 0 | x = 0 + πn, где n - любое целое число |
Вывод: простейшие тригонометрические уравнения имеют свои особенности, связанные с периодичностью тригонометрических функций, и могут иметь бесконечное количество решений. Решение таких уравнений требует применения тригонометрических тождеств и математических операций.
Решение простейших тригонометрических уравнений
Простейшие тригонометрические уравнения представляют собой уравнения, в которых переменная угла содержится только в одной функции синус, косинус или тангенс.
Для решения таких уравнений необходимо выполнить следующие шаги:
- Выразить функцию, содержащую переменный угол, в виде равенства нулю.
- Решить полученное уравнение, найдя все значения угла, при которых функция равна нулю.
- Определить значения угла, удовлетворяющие заданным условиям.
Рассмотрим пример решения простейшего тригонометрического уравнения:
| Пример | Решение |
|---|---|
| sin(x) = 0 | x = 0 + k * π, где k - целое число |
Данное уравнение имеет бесконечное множество решений, которые образуют арифметическую прогрессию с шагом π.
Важно учесть особенности и ограничения функций, например, область определения или периодичность. Иногда не все решения окажутся допустимыми.
Таким образом, решение простейших тригонометрических уравнений требует тщательного анализа условий задачи и использования соответствующих формул и свойств тригонометрических функций.
Простейшие тригонометрические уравнения с особыми случаями
A*sin(x) + B*cos(x) = C,
где A, B и C - некоторые произвольные числа.
При решении таких уравнений возможно несколько особых случаев, которые требуют отдельного рассмотрения.
| Особый случай | Условия | Решение |
|---|---|---|
| Уравнение с A = 0 и B = 0 | 0 = C | x = arcsin(C) + 2πk |
| Уравнение с A = 0 и B ≠ 0 | B*cos(x) = C | x = arccos(C/B) + 2πk |
| Уравнение с A ≠ 0 и B = 0 | A*sin(x) = C | x = arcsin(C/A) + 2πk |
| Уравнение с A = -B | A*sin(x) - A*sin(x) = C | x = π/2 + arcsin(-C/A) + 2πk |
Здесь k - целое число.
В каждом из этих случаев необходимо учитывать особенности рассмотренных функций - синуса и косинуса. Производя дополнительные преобразования и учет ограничений на область определения данных функций, можно получить конкретные значения их аргументов.
Частные случаи простейших тригонометрических уравнений: типы и решения
Простейшие тригонометрические уравнения часто встречаются в математике и имеют широкое применение в различных областях, включая физику, инженерию и естественные науки. Частные случаи этих уравнений представляют собой особые ситуации, которые требуют дополнительного анализа и решения.
Существует несколько типов частных случаев простейших тригонометрических уравнений, которые можно выделить:
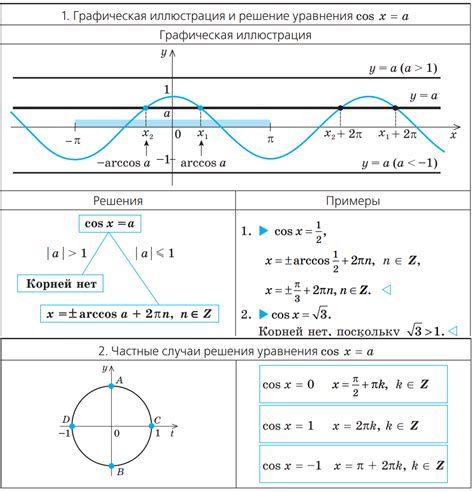
1. Уравнения синуса и косинуса: эти уравнения имеют вид sin(x) = a или cos(x) = a, где a - конкретное значение. Чтобы решить такое уравнение, необходимо найти все значения x, которые удовлетворяют условию. Для этого можно использовать обратные функции синуса и косинуса - arcsin и arccos.
2. Уравнения тангенса и котангенса: эти уравнения представляют собой tan(x) = a или cot(x) = a, где a - конкретное значение. Для их решения можно использовать обратные функции тангенса и котангенса - arctan и arccot.
3. Уравнения секанса и косеканса: такие уравнения имеют вид sec(x) = a или csc(x) = a, где a - конкретное значение. Для их решения можно использовать обратные функции секанса и косеканса - arcsec и arccsc.
Каждый из этих типов частных случаев имеет свои специфические методы решения. Обычно решение состоит в нахождении обратной функции, а затем нахождении всех значений x, которые удовлетворяют уравнению. Для уравнений с дополнительными условиями могут потребоваться дополнительные шаги, например, ограничения на диапазон значений x.
Важно отметить, что решение частных случаев простейших тригонометрических уравнений может иметь одно или несколько решений, а также может содержать особые случаи, например, когда уравнение не имеет решений или имеет бесконечное количество решений.
Практическое применение решения частных случаев тригонометрических уравнений

Решение частных случаев тригонометрических уравнений имеет множество практических применений в различных областях науки и инженерии. Тригонометрические уравнения возникают во многих задачах и позволяют нам анализировать и решать сложные взаимосвязи и закономерности.
Одним из практических применений решения частных случаев тригонометрических уравнений является измерение расстояний и высот. Например, при помощи теодолита и тригонометрических уравнений можно определить высоту недоступных объектов, таких как здания или горы, используя углы и расстояния между точками измерения.
Тригонометрические уравнения также активно применяются в физике и инженерии, в том числе при моделировании колебаний и волн, электрических и магнитных полей, акустики и оптики. Задачи на решение тригонометрических уравнений встречаются в механике, астрономии и других естественных науках.
Благодаря развитию компьютерных технологий и математических программ, решение тригонометрических уравнений стало доступным и простым в использовании. Программы, такие как Mathematica, Matlab и другие, способны решать сложные тригонометрические уравнения и предоставляют результаты с высокой точностью.
В целом, решение частных случаев тригонометрических уравнений является неотъемлемой частью математического анализа и находит широкое применение в научных и инженерных исследованиях, а также в повседневной практике при решении реальных задач.








